题目内容
已知数列 中,
中, .
.
(Ⅰ)设 ,求数列
,求数列 的通项公式;
的通项公式;
(Ⅱ)设 求证:
求证: 是递增数列的充分必要条件是
是递增数列的充分必要条件是 .
.
(Ⅰ)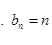 ;
;
(Ⅱ)证明:“必要性”数列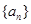 递增
递增
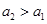
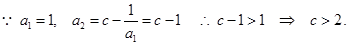
“充分性”用“数学归纳法”证明。
解析试题分析:(Ⅰ)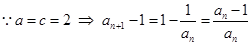

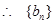 是公差为
是公差为 的等差数列,
的等差数列,
又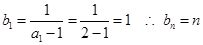 6分
6分
(Ⅱ)证明:“必要性”
数列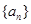 递增
递增
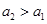
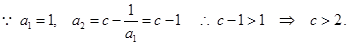 9分
9分
“充分性”
以下用“数学归纳法”证明, 时,
时, 成立
成立
①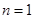 时,
时, 成立;
成立;
②假设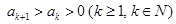 成立, 则
成立, 则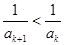
那么
即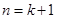 时,
时, 成立
成立
综合①②得 成立。
成立。
即 时,
时,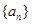 递增, 故,充分性得证。 13分
递增, 故,充分性得证。 13分
考点:本题主要考查等差数列的定义,充要条件证明问题,数学归纳法。
点评:确定数列的特征,一般要利用“定义法”或通过确定数列的通项公式,使问题得解。证明充要性问题,要证明“充分性”“必要性”两个方面,顺序上可根据难易调整。利用数学归纳法证明不等式,要注意遵循“两步一结”。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 是等差数列,
是等差数列,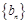 是各项均为正数的等比数列,且
是各项均为正数的等比数列,且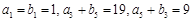
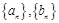 的通项公式;
的通项公式;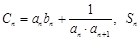 为数列
为数列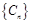 的前
的前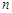 项和,求
项和,求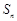 .
.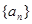 满足
满足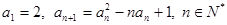 .
.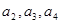 ,并由此猜想
,并由此猜想 的一个通项公式,证明你的结论;
的一个通项公式,证明你的结论;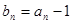 ,不等式
,不等式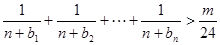 对一切
对一切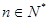 都成立,求正整数m的最大值。
都成立,求正整数m的最大值。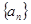 的前
的前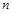 项和
项和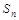 是二项式
是二项式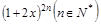 展开式中含
展开式中含 奇次幂的系数和.
奇次幂的系数和.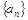 的通项公式;
的通项公式;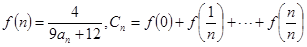 ,求
,求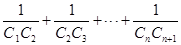 的值.
的值. 满足:
满足: (其中常数
(其中常数 ).
). 时,数列
时,数列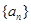 的前
的前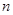 项和为
项和为 ,且
,且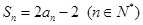 .
.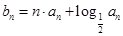 ,数列
,数列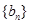 的前
的前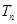 ,若不等式
,若不等式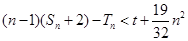 对任意
对任意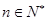 恒成立,求实数
恒成立,求实数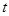 的取值范围.
的取值范围. ,其前
,其前 项和
项和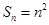 ,数列
,数列 满足
满足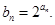
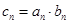 ,求数列
,求数列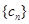 的前
的前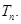
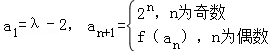 .
.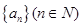 满足
满足 且对一切
且对一切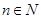 ,有
,有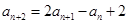
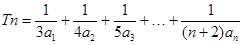 ,求
,求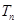 的取值范围.
的取值范围.