题目内容
已知函数f(x)的图象经过点(1,λ),且对任意x∈R,
都有f(x+1)=f(x)+2.数列{an}满足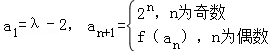 .
.
(1)当x为正整数时,求f(n)的表达式;(2)设λ=3,求a1+a2+a3+…+a2n;
(3)若对任意n∈N*,总有anan+1<an+1an+2,求实数λ的取值范围.
(1)22n+n﹣2.(2)λ的取值范围为(﹣2,+∞).
解析试题分析:解:
(1)记bn=f(n),由f(x+1)=f(x)+2有bn+1﹣bn=2对任意n∈N*都成立,
又b1=f(1)=λ,所以数列bn为首项为λ公差为2的等差数列, 2分
故bn=2n+λ﹣2,即f(n)=2n+λ﹣2. 4分
(2)由题设λ=3
若n为偶数,则an=2n﹣1;若n为奇数且n≥3,则an=f(an﹣1)=2an﹣1+λ﹣2=2•2n﹣2+λ﹣2=2n﹣1+λ﹣2=2n﹣1+1
又a1=λ﹣2=1,
即 - 6分
- 6分
a1+a2+a3++a2n=(a1+a3++a2n﹣1)+(a2+a4++a2n)=(20+22++22n﹣2+n﹣1)+(21+23++22n﹣1)
=(1+21+22++22n﹣1)+n﹣1=22n+n﹣2. 8分
(3)当n为奇数且n≥3时,an+1an+2﹣anan+1=an+1(an+2﹣an)=2n[2n+1+λ﹣2﹣(2n﹣1+λ﹣2)]=3•22n﹣1>0; 10分
当n为偶数时,an+1an+2﹣anan+1=an+1(an+2﹣an)=(2n+λ﹣2)(2n+1﹣2n﹣1)]=3•2n﹣1(2n+λ﹣2),因为anan+1<an+1an+2,所以2n+λ﹣2>0,
∵n为偶数,∴n≥2,
∵2n+λ﹣2单增∴4+λ﹣2>0,即λ>﹣2
故λ的取值范围为(﹣2,+∞). 12分
考点:数列的求和,以及数列单调性
点评:解决的关键是利用数列的通项公式以及数列的单调性来得到证明,属于中档题。

 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案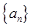 是首项
是首项 的等比数列,且
的等比数列,且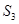 ,
,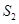 ,
, 成等差数列.
成等差数列.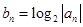 ,设
,设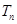 为数列
为数列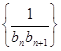 的前
的前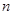 项和,若
项和,若 对一切
对一切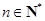 恒
恒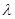 的最小值.
的最小值. 中,
中, .
. ,求数列
,求数列 的通项公式;
的通项公式; 求证:
求证: .
. 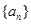 的前
的前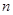 项和为
项和为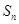 ,常数
,常数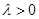 ,且
,且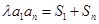 对一切正整数
对一切正整数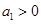 ,
,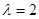 ,求证:
,求证: 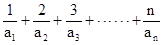 <4
<4 的前
的前 项和
项和 ,且满足
,且满足 .
. 的值,猜想
的值,猜想 是数列
是数列 的前
的前 .
.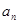 }的前
}的前 项和为
项和为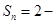

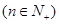
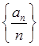 是等比数列;
是等比数列; }的前
}的前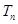 ,求
,求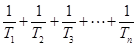 。
。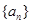 的前
的前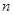 项和为
项和为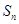 ,点
,点 在直线
在直线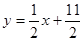 上.数列
上.数列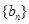 满足
满足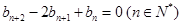 ,且
,且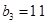 ,前9项和为153.
,前9项和为153.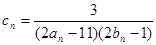 ,数列
,数列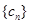 的前
的前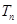 ,求使不等式
,求使不等式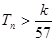 对一切
对一切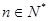 都成立的最大正整数
都成立的最大正整数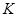 的值;
的值;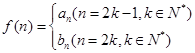 ,问是否存在
,问是否存在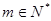 ,使得
,使得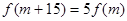 成立?若存在,求出
成立?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.  是公差
是公差 的等差数列,
的等差数列, 是各项都为正数的等比数列,且
是各项都为正数的等比数列,且 ,
, .
. …),求数列
…),求数列 的前
的前 项和
项和 .
. 的通项公式为
的通项公式为 ,数列
,数列 的前n项和为
的前n项和为 ,且满足
,且满足
 中是否存在使得
中是否存在使得 是
是