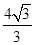题目内容
双曲线 的左焦点为F,点P为左支下半支上任意一点(异于顶点),则直线PF的斜率的变化范围是 ( )
的左焦点为F,点P为左支下半支上任意一点(异于顶点),则直线PF的斜率的变化范围是 ( )
| A.(-∞,0) | B.(1,+∞) |
| C.(-∞,0)∪(1,+∞) | D.(-∞,-1)∪(1,+∞) |
C
解析试题分析:由题意条件知双曲线的渐近线倾斜角为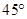 ,
,
当点P向双曲线右下方无限移动时,直线PF逐渐与渐近线平行,但是永不平行,所以倾斜角大于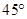 ;
;
当点P逐渐靠近顶点时,倾斜角逐渐增大,但是小于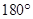 .
.
所以直线PF的倾斜角的范围是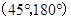 .
.
由此可知直线PF的斜率的变化范围(-∞,0)∪(1,+∞).
故选C.
考点:双曲线的几何性质,直线的斜率与倾斜角.

练习册系列答案
相关题目
椭圆 内的一点
内的一点 ,过点P的弦恰好以P为中点,那么这弦所在的直线方程
,过点P的弦恰好以P为中点,那么这弦所在的直线方程
A. | B. |
C. | D. |
过抛物线y2=4x的焦点作直线交抛物线于A(x1,y1)B(x2,y2)两点,如果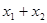 =6,那么
=6,那么 =( )
=( )
| A.6 | B.8 | C.9 | D.10 |
已知双曲线 的中心在原点,焦点在坐标轴上,
的中心在原点,焦点在坐标轴上, 是
是 上的点,且
上的点,且 是
是 的一条渐近线,则
的一条渐近线,则 的方程为( )
的方程为( )
A. | B. |
C. 或 或 | D. 或 或 |
抛物线 的焦点坐标为( )
的焦点坐标为( )
A. | B. | C. | D.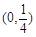 |
若椭圆 的右焦点与抛物线
的右焦点与抛物线 的焦点重合,则
的焦点重合,则 的值为 ( )
的值为 ( )
A. | B. | C. | D. |
若焦点在 轴上的双曲线
轴上的双曲线 的离心率为
的离心率为 ,则该双曲线的渐近线方程为( )
,则该双曲线的渐近线方程为( )
A. | B. | C. | D. |
 (a>b>0)的两个焦点,P是以|F1F2|为直径的圆与椭圆的一个交点,且∠PF1F2=5∠PF2F1,则该椭圆的离心率为( )
(a>b>0)的两个焦点,P是以|F1F2|为直径的圆与椭圆的一个交点,且∠PF1F2=5∠PF2F1,则该椭圆的离心率为( )
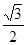


 ,弦AB中点M在准线l上的射影为
,弦AB中点M在准线l上的射影为 ,则
,则 的最大值为( )
的最大值为( )