题目内容
(本小题满分14分)
已知函数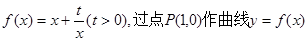 的两条切线PM、PN,切点分别为M、N.
的两条切线PM、PN,切点分别为M、N.
(I)当 时,求函数
时,求函数 的单调递增区间;
的单调递增区间;
(II)设|MN|=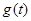 ,试求函数
,试求函数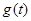 的表达式;
的表达式;
(III)在(II)的条件下,若对任意的正整数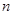 ,在区间
,在区间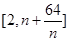 内,总存在m+1个数
内,总存在m+1个数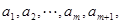 使得不等式
使得不等式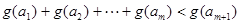 成立,求m的最大值.
成立,求m的最大值.
【答案】

(1)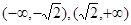 (2)
(2)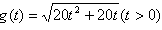 (3)6
(3)6
【解析】(I)当
 …………………1分
…………………1分
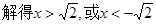 .则函数
.则函数 有单调递增区间为
有单调递增区间为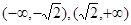 …2分
…2分
(II)设M、N两点的横坐标分别为 、
、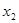 ,
,
|

同理,由切线PN也过点(1,0),得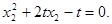 (2)
(2)
由(1)、(2),可得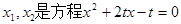 的两根,[来源:Zxxk.Com]
的两根,[来源:Zxxk.Com]
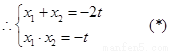 ……………………………………………………6分
……………………………………………………6分


把(*)式代入,得
因此,函数 ………………8分
………………8分
(III)易知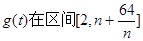 上为增函数,
上为增函数,

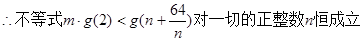 …………10分
…………10分

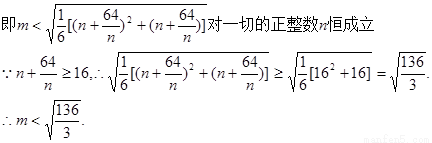
由于m为正整数,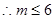 . ………………………………………………13分
. ………………………………………………13分
又当
因此,m的最大值为6. ……………………………………………………14分

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)