题目内容
函数 的图象关于点 对称.
的图象关于点 对称.
【答案】分析:将分式函数转化为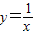 或
或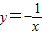 x型函数,然后利用平移关系确定函数的对称性.
x型函数,然后利用平移关系确定函数的对称性.
解答:解:由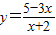 =
= ,所以函数关于点(-2,-3)对称.
,所以函数关于点(-2,-3)对称.
故答案为:(-2,-3).
点评:本题主要考查分式函数的性质,将分子常数化是解决分式函数常用的方法.
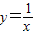 或
或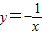 x型函数,然后利用平移关系确定函数的对称性.
x型函数,然后利用平移关系确定函数的对称性.解答:解:由
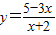 =
= ,所以函数关于点(-2,-3)对称.
,所以函数关于点(-2,-3)对称.故答案为:(-2,-3).
点评:本题主要考查分式函数的性质,将分子常数化是解决分式函数常用的方法.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目