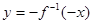题目内容
有三个函数,第一个函数是y=f(x),第二个函数是第一个函数的反函数y=f-1(x),第三个函数与第二个函数的图象关于点(1,0)对称.第三个函数是( )
分析:求出f(x)的反函数即第二个函数;据(x,y)关于点(1,0)的对称点坐标为(2-x,-y)代入第二个解析式求出第三个函数的解析式,最后求出第三个函数的反函数可得结论.
解答:解:∵第一个函数是y=f(x),它的反函数是第二个函数
∴第二个函数为y=f-1(x)
又∵第三个函数与第二个函数的图象关于点(1,0)对称
设(x,y)是第三个函数上的任意一点,则(x,y)关于点(1,0)的对称点坐标为(2-x,-y)
所以-y=f-1(2-x)
所以第三个函数解析式是y=-f-1(2-x)
它的反函数是y=2-f(-x)
故选C
∴第二个函数为y=f-1(x)
又∵第三个函数与第二个函数的图象关于点(1,0)对称
设(x,y)是第三个函数上的任意一点,则(x,y)关于点(1,0)的对称点坐标为(2-x,-y)
所以-y=f-1(2-x)
所以第三个函数解析式是y=-f-1(2-x)
它的反函数是y=2-f(-x)
故选C
点评:本题考查f(x)与f-1(x)互为反函数、考查关于关于点(1,0)的两个点的坐标的关系:(x,y)与(2-x,-y)关于点(1,0)的对称,属于基础题.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
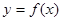 ,它的反函数是第二个函数,而第三个函数的图像与第二个函数的图像关于直线x+y=0对称,那么第三个函数是( )
,它的反函数是第二个函数,而第三个函数的图像与第二个函数的图像关于直线x+y=0对称,那么第三个函数是( )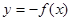 B.
B. 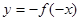 C.
C.
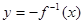 D.
D.