题目内容

【题目】已知、分别为椭圆的左、右焦点，点关于直线对称的点Q在椭圆上，则椭圆的离心率为______；若过且斜率为的直线与椭圆相交于AB两点，且，则___.

【答案】

【解析】

根据对称性和中位线判断为等腰直角三角形，根据椭圆的定义求得离心率.设根据得到，设出直线的方程，联立直线的方程和椭圆方程，根据根与系数关系列方程，解方程求得的值.

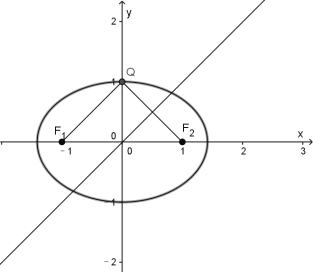
由于点关于直线对称的点Q在椭圆上，由于的倾斜角为,画出图像如下图所示，由于是坐标原点，根据对称性和中位线的知识可知为等腰直角三角形，且为短轴的端点，故离心率.不妨设，则椭圆方程化为，设直线的方程为，代入椭圆方程并化简得.设，则①，②.由于，故③.解由①②③组成的方程组得，即.

故填：（1）；（2）.

练习册系列答案
相关题目

【题目】已知函数f(x)的图象与函数h(x)＝x＋＋2的图象关于点A(0,1)对称．

(1)求函数f(x)的解析式；

(2)若g(x)＝f(x)＋，g(x)在区间(0,2]上的值不小于6，求实数a的取值范围．

【题目】在直三棱柱中，且，设其外接球的球心为O，已知三棱锥的体积为2.则球O的表面积的最小值是（）

A.B.C.D.

【题目】某微信群主发60个随机红包（即每个人抢到的红包中的钱数是随机的，且每人只能抢一个），红包被一抢而空，后据统计，60个红包中的钱数（单位：元）分配如下频率分布直方图所示（其分组区间为，，，，）.

（1）求频率分布直方图中的值及红包钱数的平均值；

（2）试估计该群中某成员抢到钱数不小于3元的概率；

（3）若该群中成员甲、乙两人都抢到4.5元红包，现系统将从抢到4元及以上红包的人中随机抽取2人，求甲、乙至少有一人被选中的概率.

【题目】已知椭圆的左右焦点分别为，离心率为，是椭圆上的一个动点，且面积的最大值为.

（1）求椭圆的方程；

（2）设直线斜率为，且与椭圆的另一个交点为，是否存在点，使得若存在，求的取值范围；若不存在，请说明理由.

【题目】在平面直角坐标系中，动点P到两点、的距离之差的绝对值等于.设点P的轨迹为C.

（1）求C的轨迹方程；

（2）过点的直线l与曲线C交于M，N两点，且Q恰好为线段的中点，求直线l的方程.

【题目】如图，在正方体中，点是线段上的动点，则下列说法错误的是（ ）

A. 当点移动至中点时，直线与平面所成角最大且为

B. 无论点在上怎么移动，都有

C. 当点移动至中点时，才有与相交于一点，记为点，且

D. 无论点在上怎么移动，异面直线与所成角都不可能是

【题目】将函数的图象向右平移个单位长度，再将所得函数图象上的所有点的横坐标缩短到原来的，得到函数的图象.已知函数的部分图象如图所示，则函数（ ）

A.最小正周期为，最大值为2

B.最小正周期为，图象关于点中心对称

C.最小正周期为，图象关于直线对称

D.最小正周期为，在区间单调递减

【题目】在直角坐标系中，以原点为极点，x轴的正半轴为极轴，以相同的长度单位建立极坐标系．己知直线的直角坐标方程为，曲线C的极坐标方程为．

（1）设t为参数，若，求直线的参数方程和曲线C的直角坐标方程；

（2）已知：直线与曲线C交于A，B两点，设，且，，依次成等比数列，求实数a的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网