题目内容
【题目】已知函数 ![]() ,
, ![]() .
. ![]() 在
在 ![]() 上有最大值9,最小值4.
上有最大值9,最小值4.
(1)求实数 ![]() 的值;
的值;
(2)若不等式 ![]() 在
在 ![]() 上恒成立,求实数
上恒成立,求实数 ![]() 的取值范围;
的取值范围;
(3)若方程 ![]() 有三个不同的实数根,求实数
有三个不同的实数根,求实数 ![]() 的取值范围.
的取值范围.
【答案】
(1)解:函数 ![]() 的对称轴为
的对称轴为 ![]() ,又
,又 ![]() ,所以
,所以 ![]() 在
在 ![]() 上单调递增,
上单调递增,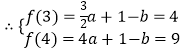 ,解得
,解得 ![]()
(2)解: ![]() ,
, ![]() ,令
,令 ![]() ,则
,则 ![]() ,
,
不等式 ![]() 可化为
可化为 ![]() ,所以,问题等价于
,所以,问题等价于 ![]() 在
在 ![]() 上恒成立,
上恒成立,
因为 ![]() ,则:
,则: ![]() ,所以:
,所以: ![]()
(3)解:令 ![]() ,图像如下:
,图像如下: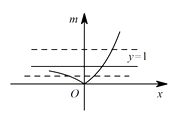
则方程 ![]() 有三个不同的实数根,等价于关于
有三个不同的实数根,等价于关于 ![]() 的方程
的方程 ![]() 有两个不等根,其中一根等于1,一根大于0且小于1,或者一根大于1,一根大于0且小于1.将
有两个不等根,其中一根等于1,一根大于0且小于1,或者一根大于1,一根大于0且小于1.将 ![]() 整理成:
整理成: ![]() ,
,
若一根等于1,一根大于0且小于1,将 ![]() 代入得
代入得 ![]() ,此时,
,此时, ![]() 只有唯一的根,不符要求,
只有唯一的根,不符要求,
所以,情况为:一根大于1,一根大于0且小于1,
令 ![]() ,则需满足
,则需满足 ![]() ,解得
,解得 ![]() .综上所述:
.综上所述: ![]() 为所求
为所求
【解析】(1)由一元二次函数的性质可得该二次函数的对称轴为x=1,故可得 f ( x ) 在 x ∈ [ 3 , 4 ] 上单调递增,结合二次函数图像的特点限制边界点的函数值进而得到关于a、b的方程组,解出其值即可。(2)由(1)的结果得到f(x) 的解析式,再由题意得到F(x)的解析式。利用整体思想设t=log2 x,根据已知的x的取值范围得出t的取值范围,由此已知的不等式即可转化为 k ≤ ![]()
![]() + 1 在 t ∈ [
+ 1 在 t ∈ [ ![]() , 2 ] 上恒成立的问题,借助二次函数在指定区间上的最值情况即可得出结果。(3)利用数形结合法结合已知条件得出方程有两个不等根,其中一根等于1,一根大于0且小于1,或者一根大于1,一根大于0且小于1,利用二次函数根的情况限制边界点的函数值,进而得到关于λ 的不等式组解出其取值范围即可。
, 2 ] 上恒成立的问题,借助二次函数在指定区间上的最值情况即可得出结果。(3)利用数形结合法结合已知条件得出方程有两个不等根,其中一根等于1,一根大于0且小于1,或者一根大于1,一根大于0且小于1,利用二次函数根的情况限制边界点的函数值,进而得到关于λ 的不等式组解出其取值范围即可。

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】2016年高一新生入学后,为了了解新生学业水平,某区对新生进行了水平测试,随机抽取了50名新生的成绩,其相关数据统计如下:
分数段 | 频数 | 选择题得分24分以上(含24分) |
[40,50) | 5 | 2 |
[50,60) | 10 | 4 |
[60,70) | 15 | 12 |
[70,80) | 10 | 6 |
[80,90) | 5 | 4 |
[90,100) | 5 | 5 |
(Ⅰ)若从分数在[70,80),[80,90)的被调查的新生中各随机选取2人进行追踪调查,求恰好有2名新生选择题得分不足24分的概率;
(Ⅱ)在(Ⅰ)的条件下,记选中的4名新生中选择题得分不足24分的人数为X,求随机变量X的分布列和数学期望.


