题目内容
【题目】已知抛物线C: ![]() ,点
,点![]() .
.
(1)求点P与抛物线C的焦点F的距离;
(2)设斜率为l的直线l与抛物线C交于A,B两点若△PAB的面积为![]() ,求直线l的方程;
,求直线l的方程;
(3)是否存在定圆M: ![]() ,使得过曲线C上任意一点Q作圆M的两条切线,与曲线C交于另外两点A,B时,总有直线AB也与圆M相切?若存在,求出m的值;若不存在,请说明理由.
,使得过曲线C上任意一点Q作圆M的两条切线,与曲线C交于另外两点A,B时,总有直线AB也与圆M相切?若存在,求出m的值;若不存在,请说明理由.
【答案】(1)P(1,0),距离为5;(2)y=x﹣1;(3)Q,存在实数m=3,使得直线AB与圆M相切.
【解析】
(1)求得抛物线的焦点坐标,由两点距离公式,计算可得所求距离;
(2)设直线l的方程为y=x+a,代入抛物线的方程,运用韦达定理和弦长公式以及三角形的面积公式,解方程可得a,进而得到直线方程;
(3)取Q(0,0),切线为y=kx,求得切点A,B,和直线AB,由相切可得m=3,证明对任意的动点Q,直线AB与圆相切,必有m=3.设Q(![]() a2,a),l:x=t(y﹣a)
a2,a),l:x=t(y﹣a)![]() a2,A(
a2,A(![]() y12,y1),B(
y12,y1),B(![]() y22,y2),运用直线和圆相切的条件和韦达定理,求得AB的方程,计算圆心到直线AB的距离,即可得证.
y22,y2),运用直线和圆相切的条件和韦达定理,求得AB的方程,计算圆心到直线AB的距离,即可得证.
(1)抛物线C:y2=4x的焦点坐标为(1,0),
则点P与抛物线C的焦点F的距离为![]() 5;
5;
(2)设直线l的方程为y=x+a,
把y=x+a方程代入抛物线y2=4x,
可得x2+2(a﹣2)x+a2=0,
∴x1+x2=4﹣2a,x1x2=a2,
∴|AB|![]() |x1﹣x2|
|x1﹣x2|
![]() 4
4![]() ,
,
点P到直线的距离d![]() ,
,
∴S△PAB![]() |AB|d
|AB|d
![]() 4
4![]() 2
2![]() ,
,
解得a=﹣1,
∴直线l的方程y=x﹣1;
(3)取Q(0,0),圆(x﹣m)2+y2=4,切线为y=kx,
由![]() 2,解得k2
2,解得k2![]() ,①
,①
将直线y=kx代入抛物线方程y2=4x,
解得A(![]() ,
,![]() ),B(
),B(![]() ,
,![]() ),
),
直线AB的方程为x![]() ,
,
若直线和圆相切,可得|![]() m|=2②
m|=2②
由①②解得m=3或2(舍去).
综上可得,对任意的动点Q,直线AB与圆相切,必有m=3.
下证m=3时,对任意的动点Q,直线AB和圆相切.
理由如下:设Q(![]() a2,a),l:x=t(y﹣a)
a2,a),l:x=t(y﹣a)![]() a2,A(
a2,A(![]() y12,y1),B(
y12,y1),B(![]() y22,y2),
y22,y2),
由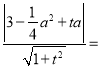 2,可得(a2﹣4)t2﹣(
2,可得(a2﹣4)t2﹣(![]() a2﹣6)at+(
a2﹣6)at+(![]() a2﹣3)2﹣4=0,
a2﹣3)2﹣4=0,
∴t1+t2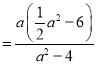 ,t1t2
,t1t2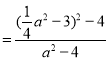 ,
,
又直线与曲线相交于A,B,
由x=t(y﹣a)![]() a2,代入抛物线方程可得y2﹣4ty+4ta﹣a2=0,
a2,代入抛物线方程可得y2﹣4ty+4ta﹣a2=0,
可得y12=4t1(y1﹣a)+a2,y22=4t2(y2﹣a)+a2,
则a,y1是方程y2=4t1(y﹣a)+a2的两根,
即有ay1=4t1a﹣a2,即为y1=4t1﹣a,同理y2=4t2﹣a.
则有A(![]() (4t1﹣a)2,4t1﹣a),B(
(4t1﹣a)2,4t1﹣a),B(![]() (4t2﹣a)2,4t2﹣a),
(4t2﹣a)2,4t2﹣a),
直线AB:y﹣(4t1﹣a)![]() (x
(x![]() (4t1﹣a)2),
(4t1﹣a)2),
即为y﹣(4t1﹣a)![]() (x
(x![]() (4t1﹣a)2),
(4t1﹣a)2),
则圆心(3,0)到直线AB的距离为
d ,
,
由(a2﹣4)t12﹣(![]() a2﹣6)at1+(
a2﹣6)at1+(![]() a2﹣3)2﹣4=0,
a2﹣3)2﹣4=0,
代入上式,化简可得d![]() 2,
2,
则有对任意的动点Q,存在实数m=3,使得直线AB与圆M相切.
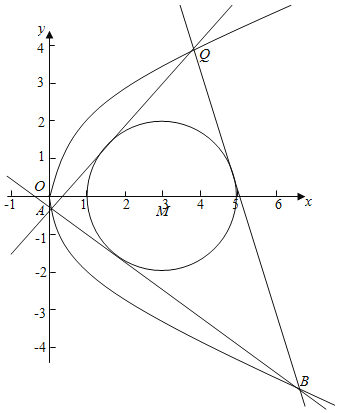

 快捷英语周周练系列答案
快捷英语周周练系列答案