题目内容
8.若$\frac{1+tanα}{1-tanα}=3+2\sqrt{2}$,则sin2α=$\frac{{2\sqrt{2}}}{3}$.分析 根据已知等式可求tanα,由万能公式即可求值.
解答 解:∵$\frac{1+tanα}{1-tanα}=3+2\sqrt{2}$,
∴整理可得:1+tanα=3-3tanα+2$\sqrt{2}$-2$\sqrt{2}$tanα,可得:tanα=$\frac{1+\sqrt{2}}{2+\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,
∴sin2α=$\frac{2tanα}{1+ta{n}^{2}α}$=$\frac{2×\frac{\sqrt{2}}{2}}{1+\frac{1}{2}}$=$\frac{{2\sqrt{2}}}{3}$.
故答案为:$\frac{{2\sqrt{2}}}{3}$.
点评 本题主要考查了万能公式和三角函数求值,属于基本知识的考查.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
18.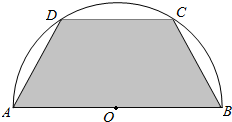 如图所示,有一块半径长为1米的半圆形钢板,现要从中截去一个内接等腰梯形部件ABCD,设梯形ABCD的面积为y平方米.
如图所示,有一块半径长为1米的半圆形钢板,现要从中截去一个内接等腰梯形部件ABCD,设梯形ABCD的面积为y平方米.
(1)设∠BOC=θ(rad),将y表示成θ的函数关系式;
(2)求y的最大值.
 如图所示,有一块半径长为1米的半圆形钢板,现要从中截去一个内接等腰梯形部件ABCD,设梯形ABCD的面积为y平方米.
如图所示,有一块半径长为1米的半圆形钢板,现要从中截去一个内接等腰梯形部件ABCD,设梯形ABCD的面积为y平方米.(1)设∠BOC=θ(rad),将y表示成θ的函数关系式;
(2)求y的最大值.
13.“a>b”是“ac2>bc2”成立的( )
| A. | 充分而非必要条件 | B. | 必要而非充分条件 | ||
| C. | 充要条件 | D. | 既非充分又非必要条件 |
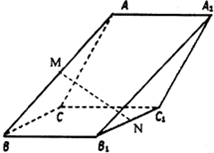 如图,在斜三棱柱ABCD-A1B1C1中,侧面ACC1A1与侧面CBB1C1都是菱形,∠B1C1C=∠C1CA=60°,AC=2,其中M,N分别是AB,B1C1的中点,
如图,在斜三棱柱ABCD-A1B1C1中,侧面ACC1A1与侧面CBB1C1都是菱形,∠B1C1C=∠C1CA=60°,AC=2,其中M,N分别是AB,B1C1的中点,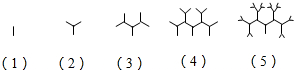 如图所示是按照一定规律画出的一列“树型”图,设第n个图有an个“树枝”,则an+1与an(n≥1)之间的关系是an+1=2an+1(n≥1).
如图所示是按照一定规律画出的一列“树型”图,设第n个图有an个“树枝”,则an+1与an(n≥1)之间的关系是an+1=2an+1(n≥1).