Question

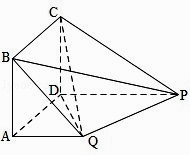
【题目】如图，四棱锥P﹣ABCD中，底面ABCD为平行四边形，∠DAB=60°，AB=2AD，PD⊥底面ABCD． （Ⅰ）证明：PA⊥BD；
（Ⅱ）若PD=AD，求二面角A﹣PB﹣C的余弦值．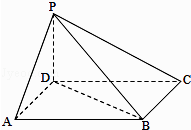

Answer 1

【答案】（Ⅰ）证明：因为∠DAB=60°，AB=2AD，由余弦定理得BD= ， 从而BD2+AD2=AB2 ， 故BD⊥AD
又PD⊥底面ABCD，可得BD⊥PD
所以BD⊥平面PAD．故PA⊥BD
（Ⅱ）如图，以D为坐标原点，AD的长为单位长，
射线DA为x轴的正半轴建立空间直角坐标系D﹣xyz，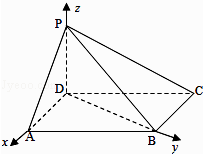

则A（1，0，0），B（0， ，0），C（﹣1， ，0），P（0，0，1）．
=（﹣1， ，0）， （0， ，﹣1）， （﹣1，0，0），
设平面PAB的法向量为 =（x，y，z），则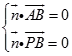
即 ，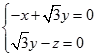
因此可取 =（ ，1， ）
设平面PBC的法向量为 =（x，y，z），则 ，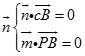
即：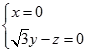
可取 =（0，1， ），cos＜ ＞=
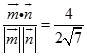
故二面角A﹣PB﹣C的余弦值为：﹣ ．
【解析】（Ⅰ）因为∠DAB=60°，AB=2AD，由余弦定理得BD= ，利用勾股定理证明BD⊥AD，根据PD⊥底面ABCD，易证BD⊥PD，根据线面垂直的判定定理和性质定理，可证PA⊥BD；（Ⅱ）建立空间直角坐标系，写出点A，B，C，P的坐标，求出向量 ，和平面PAB的法向量，平面PBC的法向量，求出这两个向量的夹角的余弦值即可．