题目内容
11.已知函数f(x)=log4(4x+1)+kx(k∈R)与g(x)=log4(a•2x-$\frac{4}{3}$a),其中f(x)是偶函数.(1)求实数k的值及f(x)的值域;
(2)求函数g(x)的定义域;
(3)若函数f(x)与g(x)的图象有且只有一个公共点,求实数a的取值范围.
分析 (1)根据偶函数的定义建立方程关系即可求k的值,化简函数,即可求出f(x)的值域;
(2)当a•2x-$\frac{4}{3}$a>0时,函数解析式有意义,分类讨论,即可求函数g(x)的定义域;
(3)根据函数f(x)与g(x)的图象有且只有一个公共点,即可得到结论.
解答 解:(1)由函数f(x)是偶函数可知f(x)=f(-x),
∴log4(4x+1)+kx=log4(4-x+1)-kx,
∴log4$\frac{{4}^{x}+1}{{4}^{-x}+1}$=-2kx,即x=-2kx对一切x∈R恒成立,
∴k=-$\frac{1}{2}$.
f(x)=log4(4x+1)-$\frac{1}{2}$x=log4(2-x+1)≥log41=0
∴f(x)的值域是[0,+∞)--------------------------------------------------------------(4分)
(2)当a•2x-$\frac{4}{3}$a>0时,函数解析式有意义
当a>0时,2x>$\frac{4}{3}$,得x>log2$\frac{4}{3}$;
当a<0时,2x<$\frac{4}{3}$,得x<log2$\frac{4}{3}$.----------------------------------------(5分)
综上,当a>0时,定义域为{x|x>log2$\frac{4}{3}$};
当a<0时,定义域为{x|x<log2$\frac{4}{3}$};---------------------------------(6分)
(3)函数f(x)与g(x)的图象有且只有一个公共点,
即方程log4(4x+1)-$\frac{1}{2}$x=log4(a•2x-$\frac{4}{3}$a)有且只有一个实根,
即方程2x+$\frac{1}{{2}^{x}}$=a•2x-$\frac{4}{3}$a,有且只有一个实根,------------------------------------(7分)
令t=2x>0,则方程(a-1)t2-$\frac{4}{3}$a-1=0有且只有一个正根,
①当a=1时,t=-$\frac{3}{4}$,不合题意;
②当a≠1时,由△=0得a=$\frac{3}{4}$或-3,
若a=$\frac{3}{4}$,则t=-2不合题意;
若a=-3,则t=$\frac{1}{2}$满足要求;----------------------------------------(8分)
若△>0,则此时方程应有一个正根与一个负根,
∴$\frac{-1}{a-1}$<0,∴a>1,又△>0得a<-3或a>$\frac{3}{4}$,∴a>1.-----------------------(9分)
综上,实数a的取值范围是{-3}∪(1,+∞).----------------------------------------(10分)
点评 本题主要考查函数奇偶性的应用,以及对数的基本运算,考查学生的运算能力,综合性较强.

| A. | (-∞,10) | B. | (-∞,10] | C. | [10,+∞) | D. | (10,+∞) |
| A. | -$\frac{3}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{1}{5}$ | D. | -$\frac{1}{5}$ |
| A. | y=x3 | B. | y=lg|x| | C. | y=-x2+1 | D. | y=2-|x| |
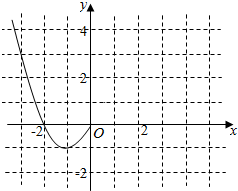 已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.
已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.