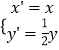题目内容
【题目】已知f(x)= ![]()
![]() ,其中
,其中 ![]() =(2cosx,﹣
=(2cosx,﹣ ![]() sin2x),
sin2x), ![]() =(cosx,1),x∈R.
=(cosx,1),x∈R.
(1)求f(x)的单调递减区间;
(2)在△ABC中,角A,B,C所对的边分别为a,b,c,f(A)=﹣1,a= ![]() ,且向量
,且向量 ![]() =(3,sinB)与
=(3,sinB)与 ![]() =(2,sinC)共线,求边长b和c的值.
=(2,sinC)共线,求边长b和c的值.
【答案】
(1)解:由题意知 ![]() .
.
∵y=cosx在a2上单调递减,∴令 ![]() ,得
,得 ![]()
∴f(x)的单调递减区间 ![]() ,
,
(2)∵ ![]() ,∴
,∴ ![]() ,又
,又 ![]() ,∴
,∴ ![]() ,即
,即 ![]() ,
,
∵ ![]() ,由余弦定理得a2=b2+c2﹣2bccosA=(b+c)2﹣3bc=7
,由余弦定理得a2=b2+c2﹣2bccosA=(b+c)2﹣3bc=7
因为向量 ![]() 与
与 ![]() 共线,所以2sinB=3sinC,由正弦定理得2b=3c.
共线,所以2sinB=3sinC,由正弦定理得2b=3c.
∴b=3,c=2.
【解析】(1)通过向量的坐标运算表示出f(x),使用二倍角公式,辅助角公式可得到f(x)=1 + 2 c o s ( 2 x + ![]() ),结合余弦函数的图象和性质可找到f(x)的单调递减区间,(2)根据f(A)=-1,可解得A的值,通过余弦定理可得到(b+c)2﹣3bc=7,由向量共线坐标的关系可得出2sinB=3sinC,通过正弦定理进行边角互化可得出2b=3c,从而可解得b和c的值.
),结合余弦函数的图象和性质可找到f(x)的单调递减区间,(2)根据f(A)=-1,可解得A的值,通过余弦定理可得到(b+c)2﹣3bc=7,由向量共线坐标的关系可得出2sinB=3sinC,通过正弦定理进行边角互化可得出2b=3c,从而可解得b和c的值.
【考点精析】关于本题考查的正弦定理的定义和余弦定理的定义,需要了解正弦定理:![]() ;余弦定理:
;余弦定理:![]() ;
;![]() ;
;![]() 才能得出正确答案.
才能得出正确答案.

练习册系列答案
相关题目