题目内容
已知函数y=f(x)为R上的奇函数,y=f(x)的导数为f'(x),且当x∈(-∞,0]时,不等式f(x)+xf'(x)<0成立,若|a+1|f(|a+1|)≥sinθf(sinθ)对一切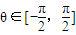 恒成立,则实数a的取值范围是 .
恒成立,则实数a的取值范围是 .
【答案】分析:根据[xf(x)]′=f(x)+xf'(x),构造函数F(x)=xf(x),由题意分析可得F(x)在(-∞,0]的单调性、奇偶性,从而可得F(x)在[0,+∞)为增函数,又由题意|a+1|f(|a+1|)≥sinθf(sinθ)对于一切θ∈[-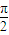 ,
,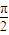 ]恒成立,则有|a+1|≥|sinθ|对于一切θ∈[-
]恒成立,则有|a+1|≥|sinθ|对于一切θ∈[-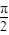 ,
,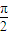 ]恒成立,又由y=sinx的性质分析可得|sinθ|的最大值为1,进而可得|a+1|≥1恒成立,解可得答案.
]恒成立,又由y=sinx的性质分析可得|sinθ|的最大值为1,进而可得|a+1|≥1恒成立,解可得答案.
解答:解:令F(x)=xf(x),则F′(x)=f(x)+xf'(x),
当x∈(-∞,0]时,不等式f(x)+xf'(x)<0成立,即F′(x)<0,
则F(x)在(-∞,0]为减函数,
又由函数y=f(x)为R上的奇函数,f(-x)=-f(x),
则F(-x)=(-x)f(-x)=xf(x)=F(x),故F(x)在R上为偶函数;
又由F(x)在(-∞,0]为减函数,则F(x)在[0,+∞)为增函数,
若|a+1|f(|a+1|)≥sinθf(sinθ)对于一切θ∈[-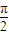 ,
,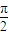 ]恒成立,
]恒成立,
则有|a+1|≥|sinθ|对于一切θ∈[-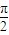 ,
,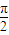 ]恒成立,
]恒成立,
而当θ∈[-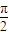 ,
,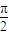 ]时,|sinθ|≤1,
]时,|sinθ|≤1,
则必有|a+1|≥1成立,
解可得,a≤-2或a≥0,即a的取值范围是(-∞,-2]∪[0,+∞);
故答案为(-∞,-2]∪[0,+∞).
点评:本题函数函数恒成立问题,涉及函数奇偶性、单调性的应用与复合函数的求导计算,关键是根据题意发现[xf(x)]′=f(x)+xf'(x),进而构造函数F(x)=xf(x),分析F(x)的单调性与奇偶性,从而解题.
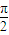 ,
,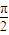 ]恒成立,则有|a+1|≥|sinθ|对于一切θ∈[-
]恒成立,则有|a+1|≥|sinθ|对于一切θ∈[-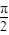 ,
,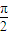 ]恒成立,又由y=sinx的性质分析可得|sinθ|的最大值为1,进而可得|a+1|≥1恒成立,解可得答案.
]恒成立,又由y=sinx的性质分析可得|sinθ|的最大值为1,进而可得|a+1|≥1恒成立,解可得答案.解答:解:令F(x)=xf(x),则F′(x)=f(x)+xf'(x),
当x∈(-∞,0]时,不等式f(x)+xf'(x)<0成立,即F′(x)<0,
则F(x)在(-∞,0]为减函数,
又由函数y=f(x)为R上的奇函数,f(-x)=-f(x),
则F(-x)=(-x)f(-x)=xf(x)=F(x),故F(x)在R上为偶函数;
又由F(x)在(-∞,0]为减函数,则F(x)在[0,+∞)为增函数,
若|a+1|f(|a+1|)≥sinθf(sinθ)对于一切θ∈[-
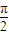 ,
,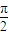 ]恒成立,
]恒成立,则有|a+1|≥|sinθ|对于一切θ∈[-
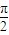 ,
,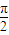 ]恒成立,
]恒成立,而当θ∈[-
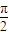 ,
,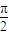 ]时,|sinθ|≤1,
]时,|sinθ|≤1,则必有|a+1|≥1成立,
解可得,a≤-2或a≥0,即a的取值范围是(-∞,-2]∪[0,+∞);
故答案为(-∞,-2]∪[0,+∞).
点评:本题函数函数恒成立问题,涉及函数奇偶性、单调性的应用与复合函数的求导计算,关键是根据题意发现[xf(x)]′=f(x)+xf'(x),进而构造函数F(x)=xf(x),分析F(x)的单调性与奇偶性,从而解题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为
已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为 已知函数y=f(x)的图象如图,则满足
已知函数y=f(x)的图象如图,则满足