题目内容
设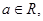 若函数
若函数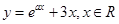 有大于零的极值点,则
有大于零的极值点,则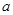 的取值为( )
的取值为( )
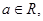 若函数
若函数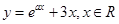 有大于零的极值点,则
有大于零的极值点,则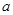 的取值为( )
的取值为( )A.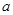 >-3 >-3 | B.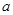 >- >- | C.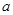 <- <- | D.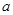 <-3 <-3 |
D
专题:综合题.
分析:求导函数,利用函数在x∈R上有大于零的极值点,可得导函数为0的方程有正根,从而可求参数a的范围.
解答:解:求导函数,可得y′=aex+3
若函数在x∈R上有大于零的极值点,即y′=aex+3=0有正根.
显然有a<0,
此时x=ln(-
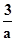 ).
).由x>0,得参数a的范围为a<-3.
综上知,a<-3.
故选D.
点评:本题考查导数知识的运用,考查函数的极值,考查解不等式,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的图像都过点P(2,0),且在点P处有相同的切线。
的图像都过点P(2,0),且在点P处有相同的切线。 的最小值。
的最小值。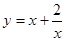 在(0,+∞)上( )
在(0,+∞)上( )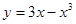 ,
,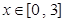 的值域是__ __
的值域是__ __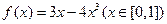 的最大值是 ▲
的最大值是 ▲
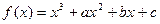 ,且知当
,且知当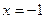 时取得极大值7,当
时取得极大值7,当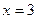 时取得极小值,试求函数
时取得极小值,试求函数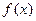 的极小值,并求
的极小值,并求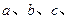 的值。
的值。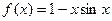 在
在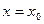 处取得极值,则
处取得极值,则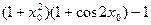 的值为( )
的值为( )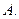 1
1 

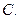 0
0 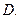 2
2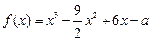
 意实数x,
意实数x,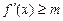 恒成立,求m的最大值;
恒成立,求m的最大值;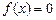 有且只有一个实根,求a的取值范围。
有且只有一个实根,求a的取值范围。