题目内容
10.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),直线l1:$\frac{x}{a}$-$\frac{y}{b}$=1被椭圆C截得的弦长为2$\sqrt{2}$,且e=$\frac{\sqrt{6}}{3}$,过椭圆C的右焦点且斜率为$\sqrt{3}$的直线l2被椭圆C截得弦长AB,(1)求椭圆的方程;
(2)弦AB的长度.
分析 (1)由直线l1:$\frac{x}{a}$-$\frac{y}{b}$=1在x轴上的截距为a,在y轴上的截距为-b,可得直线l1:$\frac{x}{a}$-$\frac{y}{b}$=1被椭圆C截得的弦长为$\sqrt{{a}^{2}+{b}^{2}}=2\sqrt{2}$,结合已知椭圆的离心率及隐含条件求得a,b,则椭圆方程可求;
(2)由题意方程求出右焦点坐标,得到直线l2的方程,联立直线方程和椭圆方程,然后利用弦长公式求得
弦AB的长度.
解答 解:(1)由直线l1:$\frac{x}{a}$-$\frac{y}{b}$=1被椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)截得的弦长为2$\sqrt{2}$,
得a2+b2=8,又$e=\frac{c}{a}=\frac{\sqrt{6}}{3}$,且a2=b2+c2,截得:a2=6,b2=2.
∴椭圆的方程为$\frac{{x}^{2}}{6}+\frac{{y}^{2}}{2}=1$;
(2)由$a=\sqrt{6}$,$\frac{c}{a}=\frac{\sqrt{6}}{3}$,得c=2.
∴椭圆C的右焦点为(2,0),
则直线l2的方程为y-0=$\sqrt{3}(x-2)$,即$y=\sqrt{3}x-2\sqrt{3}$.
联立$\left\{\begin{array}{l}{y=\sqrt{3}x-2\sqrt{3}}\\{\frac{{x}^{2}}{6}+\frac{{y}^{2}}{2}=1}\end{array}\right.$,得:5x2-18x+15=0.
设A(x1,y1),B(x2,y2),
则${x}_{1}+{x}_{2}=\frac{18}{5},{x}_{1}{x}_{2}=3$.
∴|AB|=$\sqrt{1+(\sqrt{3})^{2}}|{x}_{1}-{x}_{2}|=2\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$
=$2\sqrt{(\frac{18}{5})^{2}-4×3}=\frac{4\sqrt{6}}{5}$.
点评 本题考查了椭圆方程的求法,考查了利用弦长公式求弦长,属中档题.

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案| 学生 | 1号 | 2号 | 3号 | 4号 | 5号 |
| 甲组 | 6 | 5 | 7 | 9 | 8 |
| 乙组 | 4 | 8 | 9 | 7 | 7 |
(Ⅱ)若把上表数据对应的频率作为学生投篮命中率,规定两个小组的1号和2号同学分别代表自己的小组参加比赛,每人投篮一次,将甲活动小组两名同学投中的次数之和记作X,试求X的分布列和数学期望.
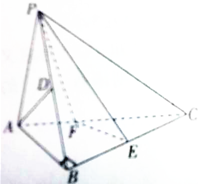 如图在三棱锥P-ABC中,已知AB⊥BC,PA⊥BC,PA=AB=BC=PB,点D,E分别为PB,BC的中点.
如图在三棱锥P-ABC中,已知AB⊥BC,PA⊥BC,PA=AB=BC=PB,点D,E分别为PB,BC的中点.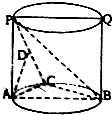 已知圆柱轴截面为PQBA,C为底面圆周上异于A、B的一点,D为PC中点.
已知圆柱轴截面为PQBA,C为底面圆周上异于A、B的一点,D为PC中点.