题目内容
已知函数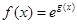 ,
, =
=  (
(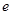 是自然对数的底)
是自然对数的底)
(1)若函数 是(1,+∞)上的增函数,求
是(1,+∞)上的增函数,求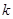 的取值范围;
的取值范围;
(2)若对任意的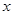 >0,都有
>0,都有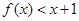 ,求满足条件的最大整数
,求满足条件的最大整数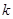 的值;
的值;
(3)证明: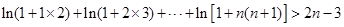 ,
, .
.
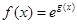 ,
, =
=  (
(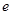 是自然对数的底)
是自然对数的底)(1)若函数
 是(1,+∞)上的增函数,求
是(1,+∞)上的增函数,求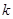 的取值范围;
的取值范围;(2)若对任意的
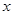 >0,都有
>0,都有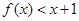 ,求满足条件的最大整数
,求满足条件的最大整数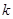 的值;
的值;(3)证明:
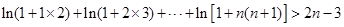 ,
, .
.解:(1)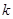 的取值范围为
的取值范围为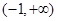 ;
;
(2)以整数k的最大值为2.
(3)略
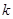 的取值范围为
的取值范围为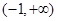 ;
; (2)以整数k的最大值为2.
(3)略
本试题主要是考查了导数在研究函数中的运用。
(1)设 因为
因为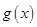 是(1,+∞)上的增函数,所以
是(1,+∞)上的增函数,所以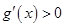 ,得到
,得到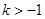 ;
;
(2)由条件得到f (1)<2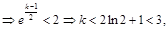 猜测最大整数
猜测最大整数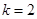 ,ging加以证明。
,ging加以证明。
(3)由(2)得到不等式
 ,结合放缩法得到结论。
,结合放缩法得到结论。
(1)设
 因为
因为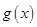 是(1,+∞)上的增函数,所以
是(1,+∞)上的增函数,所以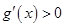 ,得到
,得到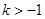 ;
;(2)由条件得到f (1)<2
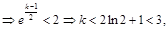 猜测最大整数
猜测最大整数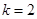 ,ging加以证明。
,ging加以证明。(3)由(2)得到不等式
 ,结合放缩法得到结论。
,结合放缩法得到结论。
练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案
相关题目
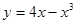 在点(-1,-3)处的切线方程是
在点(-1,-3)处的切线方程是 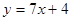
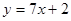
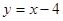
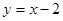
 在点
在点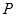 处的切线平行于直线
处的切线平行于直线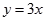 ,则点
,则点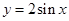 在点
在点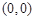 处的切线与直线
处的切线与直线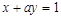 垂直,则实数
垂直,则实数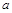 的值为( )
的值为( )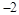
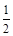
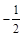
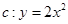 ,点
,点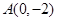 及点
及点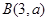 ,从点A观察B,要实现不被曲线C挡住,则实数
,从点A观察B,要实现不被曲线C挡住,则实数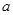 的取值范围是( )
的取值范围是( )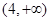
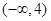
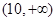
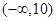
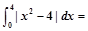 .
.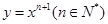 在点(1,1)处的切线与x轴的交点的横坐标为
在点(1,1)处的切线与x轴的交点的横坐标为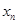 ,令
,令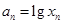 ,则
,则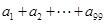 的值为
的值为 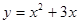 在点A(2,10)处的切线的斜率是
在点A(2,10)处的切线的斜率是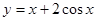 在区间
在区间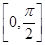 上的最大值是 .
上的最大值是 .