题目内容
(本题满分13分)
如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求B在AM上,D在AN上,对角线MN过C点,已知|AB|=3米,|AD|=2米,且受地理条件限制, 长不超过
长不超过 米。
米。

(1)要使矩形AMPN的面积大于32平方米,则AN的长应在什么范围内?
(2)若|AN| (单位:米),则当AM、AN的长度是多少时,矩形花坛AMPN的面积最大?并求出最大面积.
(单位:米),则当AM、AN的长度是多少时,矩形花坛AMPN的面积最大?并求出最大面积.
如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求B在AM上,D在AN上,对角线MN过C点,已知|AB|=3米,|AD|=2米,且受地理条件限制,
 长不超过
长不超过 米。
米。
(1)要使矩形AMPN的面积大于32平方米,则AN的长应在什么范围内?
(2)若|AN|
 (单位:米),则当AM、AN的长度是多少时,矩形花坛AMPN的面积最大?并求出最大面积.
(单位:米),则当AM、AN的长度是多少时,矩形花坛AMPN的面积最大?并求出最大面积.(1)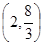 ;(2)|AN|=3米,|AM|=
;(2)|AN|=3米,|AM|=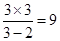 米 。
米 。
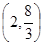 ;(2)|AN|=3米,|AM|=
;(2)|AN|=3米,|AM|=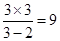 米 。
米 。本试题主要是考查了导数在研究函数中的运用。
(1)由SAMPN > 32 得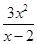 > 32 ,
> 32 ,
∴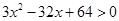 ,即(3x-8)(x-8)> 0
,即(3x-8)(x-8)> 0
∴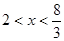 或
或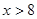 又
又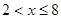 ,
,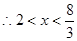
即AN长的取值范围是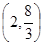
(2)令y=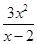 ,则y′=
,则y′=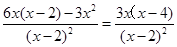
∵当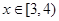 ,y′< 0,∴函数y=
,y′< 0,∴函数y=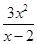 在
在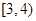 上为单调递减函数,
上为单调递减函数,
∴当x=3时y=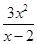 取得最大值,即
取得最大值,即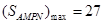 (平方米)
(平方米)
得到结论。
解:设AN的长为x米(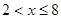 )
)
∵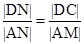 ,∴|AM|=
,∴|AM|=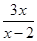
∴SAMPN=|AN|•|AM|=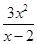 - ------------------------------------ 4分
- ------------------------------------ 4分
(1)由SAMPN > 32 得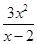 > 32 ,
> 32 ,
∴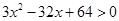 ,即(3x-8)(x-8)> 0
,即(3x-8)(x-8)> 0
∴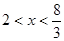 或
或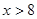 又
又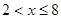 ,
,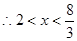
即AN长的取值范围是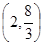 ----------- 8分
----------- 8分
(2)令y=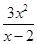 ,则y′=
,则y′=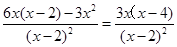 -------------- 10分
-------------- 10分
∵当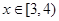 ,y′< 0,∴函数y=
,y′< 0,∴函数y=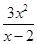 在
在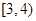 上为单调递减函数,
上为单调递减函数,
∴当x=3时y=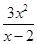 取得最大值,即
取得最大值,即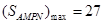 (平方米)
(平方米)
此时|AN|=3米,|AM|=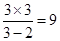 米 ……………… 13分
米 ……………… 13分
(1)由SAMPN > 32 得
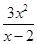 > 32 ,
> 32 ,∴
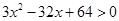 ,即(3x-8)(x-8)> 0
,即(3x-8)(x-8)> 0∴
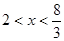 或
或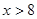 又
又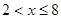 ,
,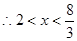
即AN长的取值范围是
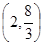
(2)令y=
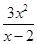 ,则y′=
,则y′=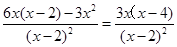
∵当
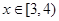 ,y′< 0,∴函数y=
,y′< 0,∴函数y=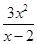 在
在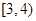 上为单调递减函数,
上为单调递减函数,∴当x=3时y=
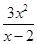 取得最大值,即
取得最大值,即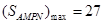 (平方米)
(平方米)得到结论。
解:设AN的长为x米(
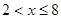 )
)∵
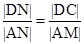 ,∴|AM|=
,∴|AM|=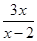
∴SAMPN=|AN|•|AM|=
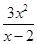 - ------------------------------------ 4分
- ------------------------------------ 4分(1)由SAMPN > 32 得
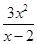 > 32 ,
> 32 ,∴
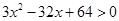 ,即(3x-8)(x-8)> 0
,即(3x-8)(x-8)> 0∴
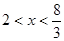 或
或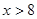 又
又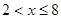 ,
,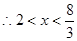
即AN长的取值范围是
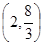 ----------- 8分
----------- 8分(2)令y=
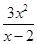 ,则y′=
,则y′=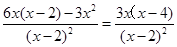 -------------- 10分
-------------- 10分∵当
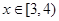 ,y′< 0,∴函数y=
,y′< 0,∴函数y=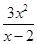 在
在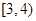 上为单调递减函数,
上为单调递减函数,∴当x=3时y=
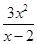 取得最大值,即
取得最大值,即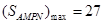 (平方米)
(平方米)此时|AN|=3米,|AM|=
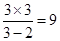 米 ……………… 13分
米 ……………… 13分
练习册系列答案
相关题目
 ),写出p与x之间的函数关系式,并说明p随x的变化情况;
),写出p与x之间的函数关系式,并说明p随x的变化情况;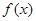 满足
满足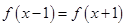 ,且在
,且在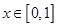 时,
时,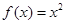 ,则关于
,则关于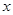 的方程
的方程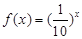 在
在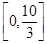 上根有
上根有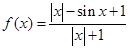
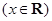 的最大值为
的最大值为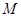 ,最小值为
,最小值为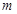 ,则
,则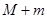 的值为 .
的值为 .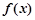 =(x-a)(x-b)(x-c),(a,b,c是两两不等的常数),则
=(x-a)(x-b)(x-c),(a,b,c是两两不等的常数),则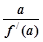 +
+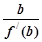 +
+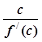 等于( )
等于( )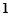
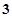
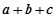
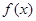 是定义在R上的偶函数,且对任意的
是定义在R上的偶函数,且对任意的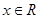 恒有
恒有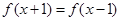 ,
,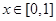 时,
时,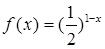 ,则其中所有正确命题的序号是_____________.
,则其中所有正确命题的序号是_____________.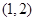 上是减函数,在
上是减函数,在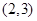 上是增函数;
上是增函数;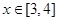 时,
时,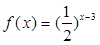 .
. 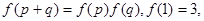
 +
+ .
.