题目内容
17.已知:空间四边形ABCD中,H、G分别是AD、CD的中点,E、F分别在BC、AB边 上,且AF=$\frac{1}{3}$AB,CE=$\frac{1}{3}$BC求证:EG、BD、FH三线共点.
分析 证明EG、BD、FH三线共点,即证明EG和FH的交点在两个平面的交线上,利用公理三可得结论.
解答 证明:如下图所示: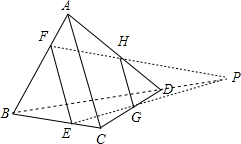
在空间四边形ABCD中,
∵H、G分别是AD、CD的中点,
∴HG∥AC,HG=$\frac{1}{2}$AC,
∵E、F分别在BC、AB边 上,且AF=$\frac{1}{3}$AB,CE=$\frac{1}{3}$BC,
∴EF∥AC,EF=$\frac{2}{3}$AC,
∴HG∥EF,HG≠EF,
即EFGH四点共线,且EG,FH不平行,
故EG,FH必相交于P,
由E,G∈平面BCD得:EG?平面BCD,
∴P∈平面BCD,
同理P∈平面BAD,
故P在平面BCD和平面BAD的交线BD上,
即EG、BD、FH三线共点.
点评 所谓线共点问题就是证明三条或三条以上的直线交于一点.(1)证明三线共点的依据是公理3.(2)证明三线共点的思路是:先证两条直线交于一点,再证明第三条直线经过该点,把问题转化为证明点在直线上的问题.实际上,点共线、线共点的问题都可以转化为点在直线上的问题来处理.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
12.直线l交椭圆$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1与M,N两点,椭圆的上顶点为B点,若△BMN的重心坐标为($\frac{1}{3}$,$\frac{1}{3}$),则直线l的方程是( )
| A. | 2x-4y+3=0 | B. | 2x-4y-3=0 | C. | 4x-2y-3=0 | D. | x-y-5=0 |
 如图,已知两个正四棱锥P-ABCD与Q-ABCD的高分别为1、2,AB=4.
如图,已知两个正四棱锥P-ABCD与Q-ABCD的高分别为1、2,AB=4.