题目内容
【题目】已知四棱锥P-ABCD的体积为 ![]() ,其三视图如图所示,其中正视图为等腰 三角形,侧视图为直角三角形,俯视图是直角梯形.
,其三视图如图所示,其中正视图为等腰 三角形,侧视图为直角三角形,俯视图是直角梯形.
(1)求正视图的面积;
(2)求四棱锥P-ABCD的侧面积.
【答案】
(1)解:如图所示四棱锥P-ABCD的高为PA,底面积为S= ![]() ·CD=
·CD= ![]() ×1=
×1= ![]()
∴四棱锥P-ABCD的体积V四棱锥P-ABCD= ![]() S·PA=
S·PA= ![]() ×
× ![]() ·PA=
·PA= ![]() ,∴PA=
,∴PA= ![]()
∴正视图的面积为S= ![]() ×2×
×2× ![]() =
= ![]() .
.
(2)解:如图所示,过A作AE∥CD交BC于E,连接PE.根据三视图可知,E是BC的中点,
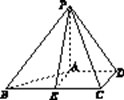
且BE=CE=1,AE=CD=1,且BC⊥AE,AB= ![]()
又PA⊥平面ABCD,∴PA⊥BC,PA⊥DC,PD= ![]() ,∴BC⊥面PAE,∴BC⊥PE,
,∴BC⊥面PAE,∴BC⊥PE,
又DC⊥AD,∴DC⊥面PAD,∴DC⊥PD,且PA⊥平面ABCD.∴PA⊥AE,
∴PE2=PA2+AE2=3.∴PE= ![]() .
.
∴四棱锥P-ABCD的侧面积为
S=S△PAB+ S△PAD+ S△PCD+ S△PBC= ![]() ·
· ![]() ·
· ![]() +
+ ![]() ·
· ![]() ·1+
·1+ ![]() ·1·
·1· ![]() +
+ ![]() ·2·
·2· ![]() =
= ![]() .
.
【解析】(I)由三视图还原直观图,关键是放在长方体中,根据三视图得到直观图,及长度大小,可得;
(II)根据棱锥的体积公式V=![]() 可得。
可得。
【考点精析】解答此题的关键在于理解由三视图求面积、体积的相关知识,掌握求体积的关键是求出底面积和高;求全面积的关键是求出各个侧面的面积,以及对由三视图还原实物图的理解,了解正视图:从前往后;侧视图:从左往右;俯视图:从上往下.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目