题目内容
17. 如图,已知直三棱柱ABC-A1B1C1中,AA1=AB=AC,AB⊥AC,M、N、Q分别是CC1,BC,AC的中点,点P在线段A1B1上运动,且A1P=λA1B1.
如图,已知直三棱柱ABC-A1B1C1中,AA1=AB=AC,AB⊥AC,M、N、Q分别是CC1,BC,AC的中点,点P在线段A1B1上运动,且A1P=λA1B1.(1)证明:无论λ取何值,总有AM⊥平面PNQ.
(2)若AC=1,试求三棱锥P-MNQ的体积.
分析 (1)建立空间直角坐标系,设出棱长,得到点的坐标,由向量数量积证得答案;
(2)把三棱锥P-MNQ的体积转化为A1-MNQ的体积,即N-A1MQ的体积,则三棱锥P-MNQ的体积可求.
解答 (1)证明: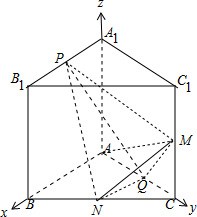
建立如图所示的空间直角坐标系,设AA1=AB=AC=a,
则A(0,0,0),M(0,a,$\frac{a}{2}$),N($\frac{a}{2},\frac{a}{2},0$),Q($0,\frac{a}{2},0$),
A1(0,0,a),B1(a,0,a),
再设P(x,0,a),由A1P=λA1B1,得$\overrightarrow{{A}_{1}P}=λ\overrightarrow{{A}_{1}{B}_{1}}$,
即(x,0,0)=λ(a,0,0),即x=λa,
∴P(λa,0,a),
∵$\overrightarrow{PN}=(\frac{a}{2}-λa,\frac{a}{2},-a)$,$\overrightarrow{PQ}=(-λa,\frac{a}{2},-a)$,$\overrightarrow{AM}=(0,a,\frac{a}{2})$,
∴$\overrightarrow{AM}•\overrightarrow{PN}=0,\overrightarrow{AM}•\overrightarrow{PQ}=0$,则AM⊥平面PNQ;
(2)解:由(1)可知,P在线段A1B1 上移动时三棱锥P-MNQ的体积一定,
不妨取A1为P,由AA1=AB=AC=1,得
${A}_{1}Q={A}_{1}M=\frac{\sqrt{5}}{2}$,MQ=$\frac{\sqrt{2}}{2}$,A1到MQ的距离为$\frac{3\sqrt{2}}{4}$,
∴${S}_{△{A}_{1}MQ}=\frac{1}{2}×\frac{\sqrt{2}}{2}×\frac{3\sqrt{2}}{4}$=$\frac{3}{8}$,QN=$\frac{1}{2}AB=\frac{1}{2}$,
则${V}_{P-MNQ}={V}_{{A}_{1}-MNQ}$=${V}_{N-{A}_{1}QM}$=$\frac{1}{3}{S}_{△{A}_{1}MQ}•QN=\frac{1}{3}×\frac{3}{8}×\frac{1}{2}=\frac{1}{16}$.
点评 利用向量知识解决立体几何问题的优点在于用代数化的方法解决立体几何,解题的关键在于用坐标表示空间向量,是中档题.

 名校课堂系列答案
名校课堂系列答案| A. | -2 | B. | -1 | C. | 0 | D. | 2 |

| A. | 4m3 | B. | 8m3 | C. | 4$\sqrt{3}$m3 | D. | 8$\sqrt{3}$m3 |