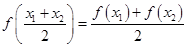题目内容
(12分)已知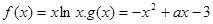
(1)求函数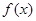 在
在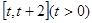 上的最小值;
上的最小值;
(2)对一切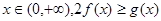 恒成立,求实数
恒成立,求实数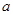 的取值范围.
的取值范围.
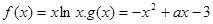
(1)求函数
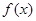 在
在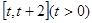 上的最小值;
上的最小值;(2)对一切
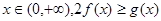 恒成立,求实数
恒成立,求实数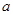 的取值范围.
的取值范围.(1)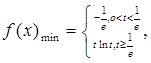 (2)a的范围是(-∞,4]。
(2)a的范围是(-∞,4]。
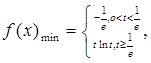 (2)a的范围是(-∞,4]。
(2)a的范围是(-∞,4]。(1)求导,利用导数对t的范围进行分类讨论求最值.
(2)本小题实质是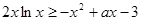 在
在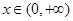 上恒成立,进一步转化为
上恒成立,进一步转化为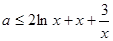 在
在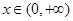 上恒成立,然后构造函数
上恒成立,然后构造函数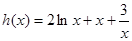 利用导数研究h(x)的最小值即可.
利用导数研究h(x)的最小值即可.
(1)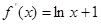 当
当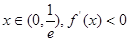
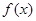 单调递减
单调递减
当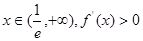
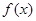 单调递增 ∵
单调递增 ∵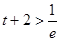
∴1°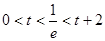 即
即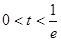 时
时 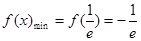
2°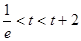 时
时 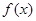 是递增的 ∴
是递增的 ∴
故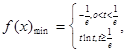
(2)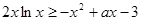 则
则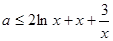 设
设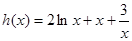
则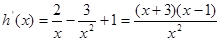
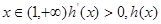 递增
递增
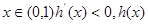 递减
递减
∴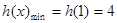 故所求a的范围是(-∞,4]
故所求a的范围是(-∞,4]
(2)本小题实质是
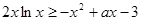 在
在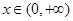 上恒成立,进一步转化为
上恒成立,进一步转化为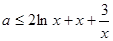 在
在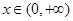 上恒成立,然后构造函数
上恒成立,然后构造函数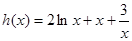 利用导数研究h(x)的最小值即可.
利用导数研究h(x)的最小值即可.(1)
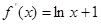 当
当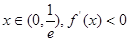
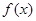 单调递减
单调递减 当
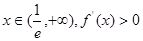
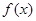 单调递增 ∵
单调递增 ∵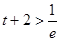
∴1°
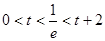 即
即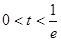 时
时 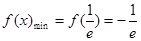
2°
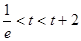 时
时 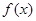 是递增的 ∴
是递增的 ∴
故
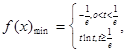
(2)
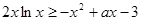 则
则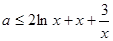 设
设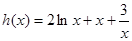
则
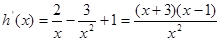
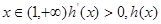 递增
递增 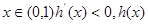 递减
递减 ∴
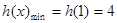 故所求a的范围是(-∞,4]
故所求a的范围是(-∞,4]
练习册系列答案
相关题目
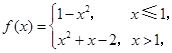 则
则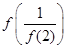 的值为( )
的值为( )



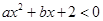 的解集为
的解集为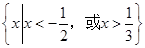 ,则
,则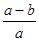 的值为( )
的值为( )

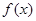 为一次函数,其图象经过点
为一次函数,其图象经过点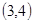 ,且
,且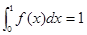 ,则函数
,则函数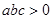 ,二次函数
,二次函数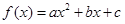 的图像可能是
的图像可能是 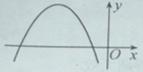
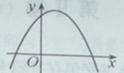
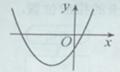
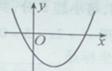
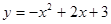 的单调递增区间是 ,
的单调递增区间是 ,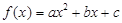 .
.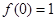 ,
,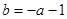 ,解关于x不等式
,解关于x不等式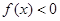 ;
;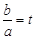 ,请把
,请把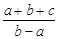 表示成关于t的函数g(t),并求g(t)的最小值.
表示成关于t的函数g(t),并求g(t)的最小值.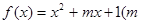 为整数)且关于
为整数)且关于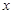 的方程
的方程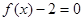 在区间
在区间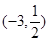 内有两个不同的实根,(1)求整数
内有两个不同的实根,(1)求整数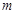 的值;(2)若
的值;(2)若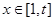 时,总有
时,总有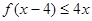 ,求
,求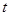 的最大值。
的最大值。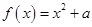 ,则下列判断正确的是( )
,则下列判断正确的是( )