题目内容
(本小题满分12分)
已知二次函数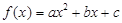 .
.
(1)若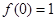 ,
,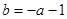 ,解关于x不等式
,解关于x不等式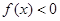 ;
;
(2)若f(x)的最小值为0,且A.<b,设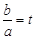 ,请把
,请把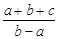 表示成关于t的函数g(t),并求g(t)的最小值.
表示成关于t的函数g(t),并求g(t)的最小值.
已知二次函数
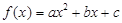 .
.(1)若
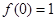 ,
,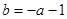 ,解关于x不等式
,解关于x不等式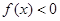 ;
;(2)若f(x)的最小值为0,且A.<b,设
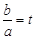 ,请把
,请把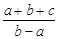 表示成关于t的函数g(t),并求g(t)的最小值.
表示成关于t的函数g(t),并求g(t)的最小值.(1)当A.>1时,解为: 1/A.<x<1 当A.=1时,解为空集。
当0<A.<1时,解为: 1<x<1/A. 当A.=1时, 解为 x>1
当A.<0时,解为: x>1或x<1/A.。
(2)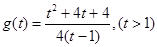 最小值为3
最小值为3
当0<A.<1时,解为: 1<x<1/A. 当A.=1时, 解为 x>1
当A.<0时,解为: x>1或x<1/A.。
(2)
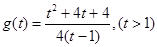 最小值为3
最小值为3本试题主要是考查了一元二次不等式的求解,以及函数的最值问题的综合运用。
(1)因为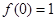 ,
,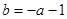 ,因此可知f(x)=
,因此可知f(x)=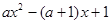 ,然后利用分类讨论得到不等式的解集。
,然后利用分类讨论得到不等式的解集。
(2)构造函数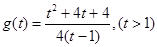 ,然后利用函数单调性质得到证明 。
,然后利用函数单调性质得到证明 。
(1)f(x)=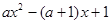
当A.>1时,解为: 1/A.<x<1 当A.=1时,解为空集。
当0<A.<1时,解为: 1<x<1/A. 当A.=1时, 解为 x>1
当A.<0时,解为: x>1或x<1/A.。
(2)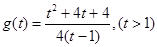 最小值为3
最小值为3
(1)因为
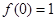 ,
,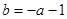 ,因此可知f(x)=
,因此可知f(x)=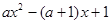 ,然后利用分类讨论得到不等式的解集。
,然后利用分类讨论得到不等式的解集。(2)构造函数
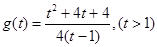 ,然后利用函数单调性质得到证明 。
,然后利用函数单调性质得到证明 。(1)f(x)=
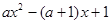
当A.>1时,解为: 1/A.<x<1 当A.=1时,解为空集。
当0<A.<1时,解为: 1<x<1/A. 当A.=1时, 解为 x>1
当A.<0时,解为: x>1或x<1/A.。
(2)
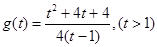 最小值为3
最小值为3
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
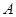 、
、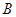 为函数
为函数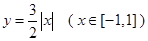 图象上不同的两个点,
图象上不同的两个点,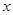 轴,又有定点
轴,又有定点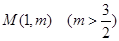 ,已知
,已知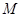 是线段
是线段 的中点.
的中点.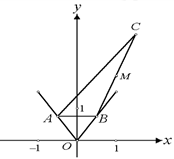
 ,写出
,写出 的面积
的面积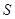 关于
关于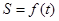 的表达式;
的表达式;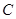 的坐标。
的坐标。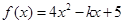 ,当
,当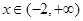 时是增函数,当
时是增函数,当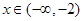 时是减函数,则
时是减函数,则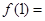 _________
_________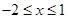 上的最小值为
上的最小值为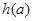 ,试将
,试将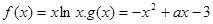
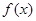 在
在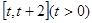 上的最小值;
上的最小值;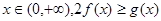 恒成立,求实数
恒成立,求实数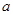 的取值范围.
的取值范围. ,
,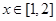 则该函数值域为( )
则该函数值域为( )

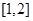
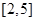
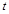 满足
满足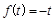 ,则称
,则称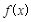 的一个次不动点.设函数
的一个次不动点.设函数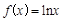 与函数
与函数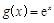 (其中
(其中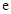 为自然对数的底数)的所有次不动点之和为
为自然对数的底数)的所有次不动点之和为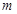 ,则
,则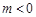
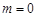
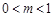
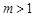
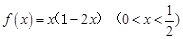 的最大值是
的最大值是