Question

如图，在正三棱柱ABC-A₁B₁C₁中已知AB=1，D在棱BB₁上，且BD=1，若AD与平面AA₁C₁C所成的角为α，则α=（　　）

• A、

  π

  3

• B、

  π

  4

• C、arcsin

  10

  4

• D、arcsin

  6

  4

Answer 1

分析：如图作DE⊥面AA₁C₁C于E，连接AE，则AD与平面AA₁C₁C所成的角为α是∠DAE，在直角三角形DAE中，算了共正弦值，再由值求角．

解答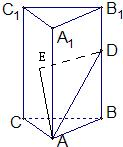：解：如图作DE⊥面AA₁C₁C于E，连接AE，
∵正三棱柱ABC-A₁B₁C₁中已知AB=1，D在棱BB₁上，且BD=1，
∴AD=

2

，DE

3

2

∴sinα=

3 2

2

=

6

4

α=arcsin

6

4

故选D．

点评：本题考点是立体几何中求线面角，这是立体几何中常考的一个题型．