题目内容
从某校高三上学期期末数学考试成绩中,随机抽取了 名学生的成绩得到频率分布直方图如下图所示:
名学生的成绩得到频率分布直方图如下图所示: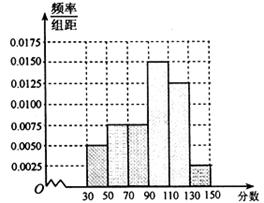
(1)根据频率分布直方图,估计该校高三学生本次数学考试的平均分(平均数的估计值等于频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标之和);
(2)若用分层抽样的方法从分数在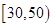 和
和 的学生中共抽取
的学生中共抽取 人,该
人,该 人中成绩在
人中成绩在 的有几人?
的有几人?
(3)在(2)中抽取的 人中,随机抽取
人中,随机抽取 人,求分数在
人,求分数在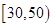 和
和 各
各 人的概率.
人的概率.
(1)92;(2)1人;(3) .
.
解析试题分析:(1)根据平均数是频率分布直方图各个小矩形的面积×底边中点横坐标之和,求出本次考试的平均分;
(2)利用频数=频率×样本数,求出分数在[30,50)和[130,150]的学生人数,再按照分层抽样的方法按比例求出3人中成绩在[130,150]的有几人;
(3)由(2)知,抽取的3人中分数在[30,50)的有2人,分数在[130,150]的有1人,问题为古典概型.
试题解析:(1)由频率分布直方图,得该校高三学生本次数学考试的平均分为
0.0050×20×40+0.0075×20×60+0.0075×20×80+0.0150×20×100
+0.0125×20×120+0.0025×20×140=92 4分
(2)样本中分数在[30,50)和[130,150]的人数分别为6人和3人
所以抽取的3人中分数在[130,150]的人有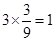 (人) 8分
(人) 8分
(3)由(2)知:抽取的3人中分数在[30,50)的有2人,记为
分数在[130,150]的人有1人,记为 ,从中随机抽取2人
,从中随机抽取2人
总的情形有 三种.
三种.
而分数在[30,50)和[130,150]各1人的情形有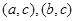 两种
两种
故所求概率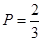 12分.
12分.
考点:1.频率分布直方图;2.分层抽样;3.古典概型.

电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查,如图是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图.将日均收看该体育节目时间不低于40分钟的观众称为“体育”.
根据已知条件完成下面的2×2列联表:
| 是否体育迷 性别 | 非体育迷 | 体育迷 | 总计 |
| 男 | ( _________ ) | ( _________ ) | 45 |
| 女 | ( _________ ) | 10 | 55 |
| 总计 | ( _________ ) | ( _________ ) | 100 |

某汽车厂生产的A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆)
| | 轿车A | 轿车B | 轿车C |
| 舒适性 | 800 | 450 | 200 |
| 标准型 | 100 | 150 | 300 |
(Ⅰ)在这个月生产的轿车中,用分层抽样的方法抽取n辆,其中有A类轿车45辆,求n的值;
(Ⅱ)在C类轿车中,用分层抽样的方法抽取一个容量为5的样本,将该样本看成一个总体,从中任取2辆,求至少1辆舒适型轿车的概率;
(Ⅲ)用随机抽样的方法从A类舒适型轿车中抽取10辆,经检测它们的得分如下:,8.7,9.3,8.2,9.4,8.6,9.2,9.6,9.0,8.4,8.6,把这10辆轿车的得分看作一个总体,从中任取一个数,求该数与总体平均数之差的绝对值超过0.6的概率.
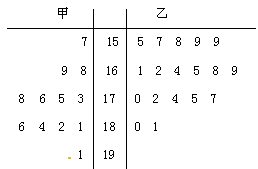
随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm)获得身高数据如下:
| 甲班: | 158 | 168 | 162 | 168 | 163 | 170 | 182 | 179 | 171 | 179 |
| 乙班: | 159 | 168 | 162 | 170 | 165 | 173 | 176 | 181 | 178 | 179 |
(1)完成数据的茎叶图(以百位十位为茎,以个位为叶),并求甲班样本数据的中位数、众数;
(2)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率。
某地区2007年至2013年农村居民家庭纯收入y(单位:千元)的数据如下表:
| 年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
| 年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求y关于t的线性回归方程;
(2)利用(1)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
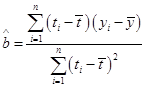 ,
,
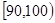 ,第二组
,第二组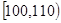 , ,第五组
, ,第五组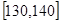 .按上述分组
.按上述分组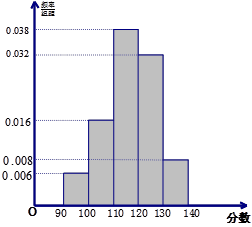
 ,否则视为违规扣分.某天,
,否则视为违规扣分.某天,