题目内容
某校50名学生参加2013年全国数学联赛初赛,成绩全部介于90分到140分之间.将成绩结果
按如下方式分成五组:第一组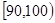 ,第二组
,第二组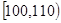 , ,第五组
, ,第五组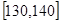 .按上述分组
.按上述分组
方法得到的频率分布直方图如图所示.
(1)若成绩大于或等于100分且小于120分认为是良好的,求该校参赛学生在这次数学联赛中成绩良好
的人数;
(2)若从第一、五组中共随机取出两个成绩,求这两个成绩差的绝对值大于30分的概率.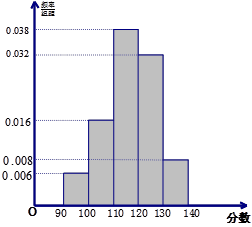
(1)27;(2)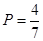 .
.
解析试题分析:(1)关键是从频率分布直方图中提取数据信息,进行统计与概率的正确运算;(2)古典概型的概率问题,关键是正确找出基本事件总数和所求事件包含的基本事件数,然后利用古典概型的概率计算公式计算;(3)当基本事件总数较少时,用列举法把所有的基本事件一一列举出来,要做到不重不漏,有时可借助列表,树状图列举,当基本事件总数较多时,注意去分排列与组合;(4)注意判断是古典概型还是几何概型,基本事件前者是有限的,后者是无限的,两者都是等可能性.
试题解析:(1)由频率分布直方图知,成绩在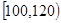 内的人数为:
内的人数为: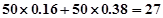 (人)
(人)
所以该班成绩良好的人数为27人. 5分
(2)由频率分布直方图知,成绩在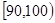 的人数为
的人数为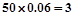 人,设为
人,设为 、
、 、
、 ;
;
成绩在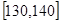 的人数为
的人数为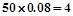 人,设为
人,设为 、
、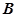 、
、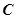 、
、 .
.
若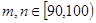 时,有
时,有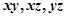 3种情况;
3种情况;
若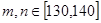 时,有
时,有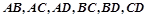 6种情况;
6种情况;
若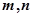 分别在
分别在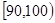 和
和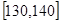 内时,共有12种情况.
内时,共有12种情况.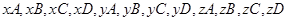
所以基本事件总数为21种,事件“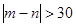 ”所包含的基本事件个数有12种.
”所包含的基本事件个数有12种.
∴ (
(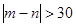 )
)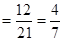 . 12分
. 12分
考点:(1)频率分布直方图的应用;(2)利用古典概型求概率.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案某校学习小组开展“学生数学成绩与化学成绩的关系”的课题研究,对该校高二年级800名学生上学期期 数学和化学成绩,按优秀和不优秀分类得结果:数学和化学都优秀的有60人,数学成绩优秀但化学不优秀的有140人,化学成绩优秀但数学不优秀的有100人.
(Ⅰ)补充完整表格并判断能否在犯错概率不超过0.001前提下认为该校学生的数学成绩与化学成绩有关系?
| | 数学优秀 | 数学不优秀 | 总计 |
| 化学优秀 | | | |
| 化学不优秀 | | | |
| 总计 | | | |
(Ⅱ)4名成员随机分成两组,每组2人,一组负责收集成绩,另一组负责数据处理。求学生甲分到负责收集成绩组,学生乙分到负责数据处理组的概率。
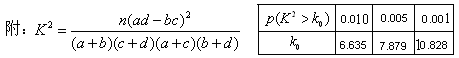
对某校小学生进行心理障碍测试得到如下的列联表:
| | 有心理障碍 | 没有心理障碍 | 总计 |
| 女生 | 10 | | 30 |
| 男生 | | 70 | 80 |
| 总计 | 20 | | 110 |
将表格填写完整,试说明心理障碍与性别是否有关?
附:

| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K | 2.072 | 2.076 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 名学生的成绩得到频率分布直方图如下图所示:
名学生的成绩得到频率分布直方图如下图所示: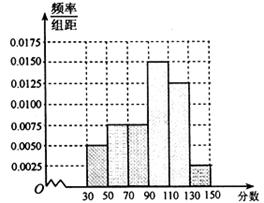
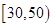 和
和 的学生中共抽取
的学生中共抽取 人,该
人,该 人,求分数在
人,求分数在 人的概率.
人的概率.  列联表;
列联表;
 和样本方差
和样本方差 (同一组的数据用该组区间的中点值作代表);
(同一组的数据用该组区间的中点值作代表); 服从正态分布
服从正态分布 ,其中
,其中 近似为样本平均数
近似为样本平均数 近似为样本方差
近似为样本方差 ;
; 表示这100件产品中质量指标值位于区间
表示这100件产品中质量指标值位于区间 的产品件数.利用(i)的结果,求
的产品件数.利用(i)的结果,求 .
.
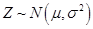 则
则 ,
, 。
。 ,则抽出的样本中女生人数是 。
,则抽出的样本中女生人数是 。 (克)(用数字作答).
(克)(用数字作答).