题目内容
用列举法表示集合:{(x,y)|y=-x2-2x+10,x∈Z,y∈N}为 .
考点:集合的表示法
专题:集合
分析:根据列举法的定义,求出集合的元素即可得到结论.
解答:解:∵y=-x2-2x+10=-(x+1)2+11,
∴当x=-1时,y=11,
当x=-2时,y=10,
当x=-3时,y=7,
当x=-4时,y=2,
当x=-5时,y=-5,此时不成立.
当x=0时,y=10,
当x=1时,y=7,
当x=2时,y=2,
当x=3时,y=-5,不成立,
∴对应的集合为{(0,10),(1,7),(2,2),(-1,11),(-2,10),(-3,7),(-4,2)}.
故答案为:{(0,10),(1,7),(2,2),(-1,11),(-2,10),(-3,7),(-4,2)}
∴当x=-1时,y=11,
当x=-2时,y=10,
当x=-3时,y=7,
当x=-4时,y=2,
当x=-5时,y=-5,此时不成立.
当x=0时,y=10,
当x=1时,y=7,
当x=2时,y=2,
当x=3时,y=-5,不成立,
∴对应的集合为{(0,10),(1,7),(2,2),(-1,11),(-2,10),(-3,7),(-4,2)}.
故答案为:{(0,10),(1,7),(2,2),(-1,11),(-2,10),(-3,7),(-4,2)}
点评:本题主要考查集合的表示,利用条件求出集合对应的元素是解决本题的关键,比较基础.

练习册系列答案
相关题目
集合{x∈N|x<5}的另一种表示法是( )
| A、{1,2,3,4} | B、{0,1,2,3,4} | C、{1,2,3,4,5} | D、{0,1,2,3,4,5} |
设集合M={x|x<2014},N={x|0<x<1},则下列关系中正确的是( )
| A、M∪N=R | B、M∩N={x|0<x<1} | C、N∈M | D、M∩N=∅ |
已知集合A={a1,a2…an},其中ak>0,(k=1,2…,n,n∈N*),集合B={(a,b)|a∈A,b∈A,a-b∈A},则集合B的元素至多有( )
| A、n个 | ||
B、
| ||
C、
| ||
| D、n2个 |
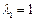 及对应的一个特征向量
及对应的一个特征向量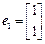 和特征值
和特征值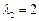 及对应的一个特征向量
及对应的一个特征向量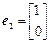 ,试求矩阵A.
,试求矩阵A.