题目内容
11.求下列函数的定义域.(1)y=lg($\frac{\sqrt{2}}{2}$-sinx).
(2)y=$\sqrt{3tanx-\sqrt{3}}$.
分析 (1)根据对数函数的性质结合三角函数解出不等式的解集即可;(2)根据二次根式的性质结合三角函数解出不等式的解集即可求出函数的定义域.
解答 解:(1)由题意得:$\frac{\sqrt{2}}{2}$-sinx>0,
解得:2kπ-$\frac{5π}{4}$<x<2kπ+$\frac{π}{4}$,
∴函数的定义域是(2kπ-$\frac{5π}{4}$,2kπ+$\frac{π}{4}$),k∈Z;
(2)由题意得:3tanx-$\sqrt{3}$≥0,
解得:kπ+$\frac{π}{6}$≤x<kπ+$\frac{π}{2}$,k∈Z.
∴函数的定义域是[kπ+$\frac{π}{6}$,kπ+$\frac{π}{2}$),k∈Z.
点评 本题考查了求函数的定义域问题,考查三角函数、对数函数的性质,是一道基础题.

练习册系列答案
相关题目
19.下列说法正确的是( )
| A. | 铺的很平的一张白纸是一个平面 | B. | 平面是矩形或平行四边形的形状 | ||
| C. | 两个平面叠在一起比一个平面厚 | D. | 平面的直观图一般画成平行四边形 |
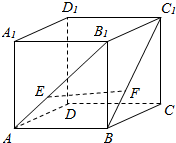 如图,正方体ABCD-A1B1C1D1,E,F分别在AB1,BC1上,且$\frac{{B}_{1}E}{AE}$=$\frac{{C}_{1}F}{BF}$=2,过EF做一个平面和面ABCD相交,并找到交线,写出作法.(注意:交线必须是由两个确定的点的连线)
如图,正方体ABCD-A1B1C1D1,E,F分别在AB1,BC1上,且$\frac{{B}_{1}E}{AE}$=$\frac{{C}_{1}F}{BF}$=2,过EF做一个平面和面ABCD相交,并找到交线,写出作法.(注意:交线必须是由两个确定的点的连线)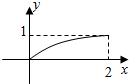 已知函数y=f(x)是定义在区间[-2,2]上的奇函数,当0≤x≤2时的图象如图所示,则y=f(x)的值域为[-1,1].
已知函数y=f(x)是定义在区间[-2,2]上的奇函数,当0≤x≤2时的图象如图所示,则y=f(x)的值域为[-1,1].