题目内容
6.在△ABC中,内角A、B、C的对边分别为a、b、c,且b2=a2+bc,A=$\frac{π}{6}$,D点在边AC上,当线段BD的长最小,则$\frac{CD}{AB}$=$\frac{1}{2}$.分析 由余弦定理可得a2=b2+c2-2bccos$\frac{π}{6}$,而b2=a2+bc,可得c=($\sqrt{3}$-1)b,a2=(2-$\sqrt{3}$)b2,利用余弦定理得出C,线段BD的长最小,BD⊥AC,则AB=2BD,CD=BD,即可得出结论.
解答 解:由余弦定理可得a2=b2+c2-2bccos$\frac{π}{6}$=b2+c2-$\sqrt{3}$bc,
∵b2=a2+bc,
∴bc+c2-$\sqrt{3}$bc=0,
解得c=($\sqrt{3}$-1)b,
a2=b2-bc=(2-$\sqrt{3}$)b2,
∴解得:cosC=$\frac{\sqrt{2}}{2}$,
∵c<b,
∴C为锐角,C=$\frac{π}{4}$.
当线段BD的长最小,BD⊥AC,则AB=2BD,CD=BD,
∴$\frac{CD}{AB}$=$\frac{1}{2}$
故答案为:$\frac{1}{2}$
点评 本题考查了余弦定理的应用,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
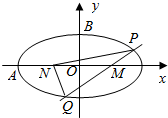 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左顶点为A,上项点为B,M(1,0),N(n,0),|MB|=$\sqrt{2}$,|AM|=3.过点M作直线l(与x轴不重合),直线l与椭圆C相交于P,Q两点,且有NP⊥NQ.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左顶点为A,上项点为B,M(1,0),N(n,0),|MB|=$\sqrt{2}$,|AM|=3.过点M作直线l(与x轴不重合),直线l与椭圆C相交于P,Q两点,且有NP⊥NQ.