题目内容
3.若方程x2sinα-y2cosα=1(0≤α<2π)表示焦点在x轴上的椭圆,则α的取值范围是( )| A. | ($\frac{3}{4}$π,π) | B. | ($\frac{π}{4}$,$\frac{3}{4}$π) | C. | ($\frac{π}{2}$,π) | D. | ($\frac{π}{2}$,$\frac{3}{4}$π) |
分析 先将原方程变成椭圆标准方程的形式为:$\frac{{x}^{2}}{-cosα}+\frac{{y}^{2}}{sinα}=\frac{1}{-cosαsinα}$,从而有$\left\{\begin{array}{l}{-cosα>0}\\{sinα>0}\\{-cosα>sinα}\end{array}\right.$,这样可通过正余弦函数的图象或三角函数线得出α的范围.
解答 解:原方程可变成:$\frac{{x}^{2}}{-cosα}+\frac{{y}^{2}}{sinα}=\frac{1}{-sinαcosα}$;
该方程表示椭圆,则:
$\left\{\begin{array}{l}{-cosα>0}\\{sinα>0}\\{-cosα>sinα}\end{array}\right.$;
∴$\frac{3}{4}π<α<π$;
∴α的取值范围是:$(\frac{3}{4}π,π)$.
故选:A.
点评 考查椭圆的标准方程的形式,椭圆的焦点,椭圆的焦点在x轴时,椭圆的方程应满足的条件,以及熟悉正余弦函数图象和三角函数线.

练习册系列答案
相关题目

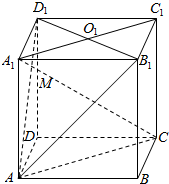 如图,O1是正方体ABCD-A1B1C1D1的面A1B1C1D1的中心,M是对角线A1C和截面B1D1A的交点,求证:O1、M、A三点共线.
如图,O1是正方体ABCD-A1B1C1D1的面A1B1C1D1的中心,M是对角线A1C和截面B1D1A的交点,求证:O1、M、A三点共线.