题目内容
【题目】若对任意![]() ,恒有
,恒有![]() ,则实数
,则实数![]() 的最小值为( )
的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
不等式![]() 两边同时乘以
两边同时乘以![]() ,等价变形为
,等价变形为![]() ,利用
,利用![]() ,
,![]() ,将不等式变形为
,将不等式变形为![]() ,构造函数
,构造函数![]() ,不等式变形为
,不等式变形为![]() ,利用导数判断函数
,利用导数判断函数![]() 在
在![]() 上单调递增,从而确定
上单调递增,从而确定![]() 在
在![]() 恒成立,即
恒成立,即![]() 在
在![]() 恒成立.构造新函数
恒成立.构造新函数![]() ,利用导数求函数
,利用导数求函数![]() 的最大值,确定
的最大值,确定![]() 的取值范围,即可.
的取值范围,即可.
由题意可知,不等式![]() 变形为
变形为![]() .
.
设![]() ,
,
则![]()
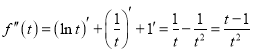 .
.
当![]() 时
时![]() ,即
,即![]() 在
在![]() 上单调递减.
上单调递减.
当![]() 时
时![]() ,即
,即![]() 在
在![]() 上单调递增.
上单调递增.
则![]() 在
在![]() 上有且只有一个极值点
上有且只有一个极值点![]() ,该极值点就是
,该极值点就是![]() 的最小值点.
的最小值点.
所以![]() ,即
,即![]() 在
在![]() 上单调递增.
上单调递增.
若使得对任意![]() ,恒有
,恒有![]() 成立.
成立.
则需对任意![]() ,恒有
,恒有![]() 成立.
成立.
即对任意![]() ,恒有
,恒有![]() 成立,则
成立,则![]() 在
在![]() 恒成立.
恒成立.
设![]() 则
则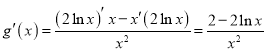 .
.
当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 上单调递增
上单调递增
当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 上单调递减
上单调递减
则![]() 在
在![]() 上有且只有一个极值点
上有且只有一个极值点![]() ,该极值点就是
,该极值点就是![]() 的最大值点.
的最大值点.
所以![]() ,即
,即![]() ,则实数
,则实数![]() 的最小值为
的最小值为![]() .
.
故选:D

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
【题目】为了调查某大学学生的某天上网的时间,随机对![]() 名男生和
名男生和![]() 名女生进行了不记名的问卷调查.得到了如下的统计结果:
名女生进行了不记名的问卷调查.得到了如下的统计结果:
表1:男生上网时间与频数分布表
上网时间(分钟) |
|
|
|
|
|
人数 |
|
|
|
|
|
表2:女生上网时间与频数分布表
上网时间(分钟) |
|
|
|
|
|
人数 |
|
|
|
|
|
(1)用分层抽样在![]() 选取
选取![]() 人,再随机抽取
人,再随机抽取![]() 人,求抽取的
人,求抽取的![]() 人都是女生的概率;
人都是女生的概率;
(2)完成下面的![]() 列联表,并回答能否有
列联表,并回答能否有![]() 的把握认为“大学生上网时间与性别有关”?
的把握认为“大学生上网时间与性别有关”?
上网时间少于 | 上网时间不少于 | 合计 | |
男生 | |||
女生 | |||
合计 |
附: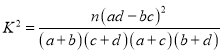
|
|
|
|
|
|
|
|
|
|
|
|