题目内容
 (本题满分14分)如图,已知二次函数
(本题满分14分)如图,已知二次函数![]() ,直线l
,直线l![]() :x = 2,直线l
:x = 2,直线l![]() :y = 3tx(其中
:y = 3tx(其中![]() 1< t < 1,t为常数);若直线l
1< t < 1,t为常数);若直线l![]() 、l
、l![]() 与函数
与函数![]() 的图象所围成的封闭图形如图(5)阴影所示.(1)求y =
的图象所围成的封闭图形如图(5)阴影所示.(1)求y = ![]() ;(2)求阴影面积s关于t的函数s = u(t)的解析式;(3)若过点A(1,m)(m≠4)可作曲线s=u(t)(t∈R)的三条切线,求实数m的取值范围.
;(2)求阴影面积s关于t的函数s = u(t)的解析式;(3)若过点A(1,m)(m≠4)可作曲线s=u(t)(t∈R)的三条切线,求实数m的取值范围.
(Ⅰ) ![]() (Ⅱ)
(Ⅱ) ![]()
解析:
(1)由图可知二次函数的图象过点(0,0),(1,0),
则![]() ,又因为图象过点(2,6),∴6=2
,又因为图象过点(2,6),∴6=2![]() ,
,![]() , 3分
, 3分
∴函数![]() 的解析式为
的解析式为![]() ;…4分
;…4分
(2)由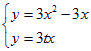 得
得![]() ,
,
![]() ∴直线
∴直线![]() 与
与![]() 的图象的交点横坐标分别为0,
的图象的交点横坐标分别为0,![]() ,…6分
,…6分
由定积分的几何意义知:![]()
![]()
![]() ,…8分
,…8分
∵曲线方程为![]()
∴点![]() 不在曲线上,设切点为,则点
不在曲线上,设切点为,则点![]() 的坐标满足:
的坐标满足:
![]() 因
因![]() ,故切线的斜率为:
,故切线的斜率为:
![]() ,整理得
,整理得![]() ,…10分
,…10分
∵过点![]() 可作曲线的三条切线,∴关于
可作曲线的三条切线,∴关于![]() 方程
方程![]() 有三个实根.
有三个实根.
设![]() ,则
,则![]() ,由
,由![]() 得
得![]() ,
,
∵当![]() 时,
时,![]() 在
在![]() 在上单调递增,
在上单调递增,
∵当![]() 时,
时,![]() 在
在![]() 上单调递减.
上单调递减.
∴函数![]() 的极值点为
的极值点为![]() ,…12分
,…12分
∴关于![]() 当成
当成![]() 有三个实根的充要条件是
有三个实根的充要条件是![]() ,
,
解得![]() ,故所求的实数
,故所求的实数![]() 的取值范围是
的取值范围是![]() ,……14分
,……14分

练习册系列答案
相关题目


 、
、 的边长都是1,平面
的边长都是1,平面 平面
平面 在
在 上移动,点
上移动,点 在
在 上移动,若
上移动,若 (
( )
)
 的长;
的长; 为何值时,
为何值时, 与面
与面 所成锐二面角余弦值的大小.
所成锐二面角余弦值的大小. ,又E、F分别是C1A和C1B的中点。
,又E、F分别是C1A和C1B的中点。 (1)求证:EF//平面ABC;
(1)求证:EF//平面ABC; 平面C1CBB1;
平面C1CBB1;