题目内容

在函数y=log3x的图象上取横坐标分别为a，a+2，a+4，（a＞1）的三点A、B、C，设△ABC的面积为S，求证：S＜log3
9
5
．
证明：由函数y=log3x
得f（a）=log3a，
f（a+2）=log3a+2，
f（a+4）=log3a+4
根据题意：
S=
1
2
（f（a）+2f（a+2）+f（a+4））×2-
1
2
（f（a）+f（a+4））×4
=
1
2
（log3a+2log3（a+2）+log3（a+4）×2-
1
2
（log3a+log3（a+4））×4
=
log(
(a+2)2
a(a+4)
)3
=
log(1+
4
(a+2)2-4
)3
＜
log
9
5
3
练习册系列答案
相关题目
函数y=log
1
2
(2x-4)的定义域是（　　）
A．[2，+∞）B．（-∞，2]C．（-∞，-2）D．（2，+∞）
已知x、y为正实数，且lg2x+lg8y=lg4，则
1
x
+
3
y
的最小值是（　　）
A．4B．8C．12D．16
计算：
（1）(
32
×
3
)6+（
2×
2
）
4
3
-（-2008）0；
（2）lg
1
2
-lg
5
8
+lg12.5-log89×log278．
（1）计算：(
32
)6-
7
5
×(
25
49
)
1
2
-(-2013)0
（2）已知log73=a，log74=b，用a，b表示log4948．
若（㏒23）x-（㏒53）-y≥（㏒23）-x-（㏒53）y，则（　　）
A．x+y≤0B．x+y≥0C．x-y≥0D．x-y≤0
函数f(x)=log
1
2
(x2-6x+5)在（a，+∞）上是减函数，则实数a的最小值是______．
已知log3m＞log3n，则（　　）
A．m＞nB．m＜nC．m=nD．以上都不对
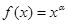已知幂函数的部分对应值如下表：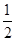
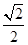
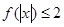x
1

f(x)
1

 
则不等式的解集是(　　)．
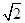A．{x|－4≤x≤4}              B．{x|0≤x≤4}
C．{x|－≤x≤}         D．{x|0<x≤}

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网