题目内容
若(㏒23)x-(㏒53)-y≥(㏒23)-x-(㏒53)y,则( )
| A.x+y≤0 | B.x+y≥0 | C.x-y≥0 | D.x-y≤0 |
(㏒23)x-(㏒53)-y≥(㏒23)-x-(㏒53)y
因为log23>log35>1
而当a>1时,f(x)=ax-a-x为递增函数
所以x≥-y
x+y≥0
故选B.
因为log23>log35>1
而当a>1时,f(x)=ax-a-x为递增函数
所以x≥-y
x+y≥0
故选B.

练习册系列答案
相关题目
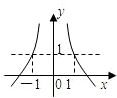
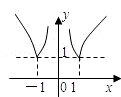
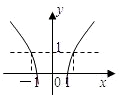
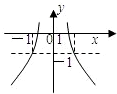
 ,则满足
,则满足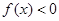 的
的 取值范围是 .
取值范围是 .