题目内容
已知△ABC的三个内角A、B、C所对的边分别为a、b、c,向量m=(1,1-sinA),n =(cosA,1),且m^ n.
=(cosA,1),且m^ n.
(Ⅰ)求角A;
(Ⅱ)若b+c=a,求sin(B+)的值.
 =(cosA,1),且m^ n.
=(cosA,1),且m^ n.(Ⅰ)求角A;
(Ⅱ)若b+c=a,求sin(B+)的值.
(1) A=.
(2)
解:(1)因为m^ n,所以m·n=0即cosA+1-sinA=0. ……2分
所以sinA-cosA=1,即sin(A-)=. ……5分
有因为0<A<π,所以-<A-<,所以A-=即A=.……6分
(2)因为b+c=a,由正弦定理得sinB+sinC=sinA=.……8分
因为B+C=,所以sinB+sin(-B)=.化简得sinB+cosB=,
即sin(B+)=.12分
所以sinA-cosA=1,即sin(A-)=. ……5分
有因为0<A<π,所以-<A-<,所以A-=即A=.……6分
(2)因为b+c=a,由正弦定理得sinB+sinC=sinA=.……8分
因为B+C=,所以sinB+sin(-B)=.化简得sinB+cosB=,
即sin(B+)=.12分

练习册系列答案
相关题目

 (如图3)进行野炊训练. 已知
(如图3)进行野炊训练. 已知 ,
, 、
、 两点间距离为
两点间距离为 .
. 与地面
与地面 所成角的大小(用反三角函
所成角的大小(用反三角函 数值表示)
数值表示) ;
; ,用吊绳
,用吊绳 将炊事锅吊起烧水(锅的大小忽略不计),若使炊事锅
将炊事锅吊起烧水(锅的大小忽略不计),若使炊事锅 ,试问吊绳
,试问吊绳 中,
中, ,
,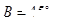 ,则角
,则角 等于
等于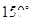
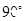
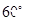
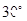
 .
. 的值;
的值; 的值。
的值。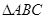 中,a=1,b=
中,a=1,b= , A=30°,则B等于 ( )
, A=30°,则B等于 ( ) ,AC=14,DC=6,求AD的长.
,AC=14,DC=6,求AD的长. 分别是△
分别是△ 的三个内角
的三个内角 ,
, ,
,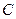 所对的边,若
所对的边,若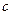 =2,
=2, =
= ,
,  ,则
,则 =" " .
=" " . 图象的相邻两条对称轴间的距离为
图象的相邻两条对称轴间的距离为 ,且图象上一个最高点的坐标为
,且图象上一个最高点的坐标为
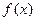 的解析式;
的解析式; 的值。
的值。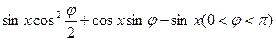 在
在 处取最小值.
处取最小值.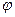 的值;
的值;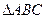 中,
中,  分别是角A,B,C的对边,已知
分别是角A,B,C的对边,已知
 ,求角C.
,求角C.