题目内容
【题目】如图,四棱锥P﹣ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E是PD的中点. 
(1)证明:PB∥平面AEC;
(2)设AP=1,AD= ![]() ,三棱锥P﹣ABD的体积V=
,三棱锥P﹣ABD的体积V= ![]() ,求A到平面PBC的距离.
,求A到平面PBC的距离.
(3)在(2)的条件下求直线AP与平面PBC所成角的正弦值.
【答案】
(1)证明:设BD和AC交于点O,连接EO.
∵ABCD为矩形,∴O为BD的中点.
又∵E为PD的中点,∴EO∥PB
∵EO平面AEC,PB平面AEC,
∴PB∥平面AEC.
(2)解:VP﹣ABD= ![]() PAABAD=
PAABAD= ![]() AB.由V=
AB.由V= ![]() ,可得AB=
,可得AB= ![]()
作AH⊥PB交PB于H.
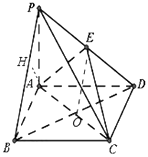
由BC⊥AB,BC⊥PA,知BC⊥平面PAB.
∴BC⊥AH,故AH⊥平面PBC.
又AH= ![]() =
= ![]() .
.
∴A到平面PBC的距离为 ![]() .
.
(3)解:由(2)可知:AH⊥平面PBC.
∴∠APH为直线AP与平面PBC所成角
在Rt△APH中,AH= ![]() ,AP=1,
,AP=1,
∴sin∠APH= ![]() =
= ![]() .
.
∴直线AP与平面PBC所成角的正弦值为 ![]() .
.
【解析】(1)设BD和AC交于点O,连接EO.运用三角形的中位线定理和线面平行的判定定理,即可得证;(2)运用棱锥的体积公式,求得AB,作AH⊥PB交PB于H,证得AH⊥平面PBC,运用直角三角形PAB中面积相等,可得AH的长,即为所求;(3)推得∠APH为直线AP与平面PBC所成角,在Rt△APH中,运用正弦函数的定义,计算即可得到所求值.
【考点精析】解答此题的关键在于理解空间角的异面直线所成的角的相关知识,掌握已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则 .
.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案
相关题目
