Question

17．函数y=f（x）（x∈R）的图象如图所示，则函数g（x）=f（log${\;}_{\frac{1}{2}}$x）的单调增区间是[1，$\sqrt{2}$]．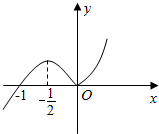

Answer 1

分析 令t=$lo{g}_{\frac{1}{2}}x$，求出内函数对数函数的定义域，结合外函数的图象求出外函数的两个极值点，然后根据复合函数单调性满足的原则求得函数g（x）=f（log${\;}_{\frac{1}{2}}$x）的单调增区间．

解答 解：令t=$lo{g}_{\frac{1}{2}}x$，则x＞0，
由$lo{g}_{\frac{1}{2}}x=0$，解得x=1；
由$lo{g}_{\frac{1}{2}}x=-\frac{1}{2}$，解得：x=$\sqrt{2}$．
∵内层函数t=$lo{g}_{\frac{1}{2}}x$为减函数，
外函数y=f（x）在（-∞，-$\frac{1}{2}$），（0，+∞）上为增函数，在[-$\frac{1}{2}$，0]上为减函数，
由复合函数的单调性可得：函数g（x）=f（log${\;}_{\frac{1}{2}}$x）的单调增区间是[1，$\sqrt{2}$]．
故答案为：[1，$\sqrt{2}$]．

点评 本题考查复合函数的单调性，复合的两个函数同增则增，同减则减，一增一减则减，注意对数函数的定义域是求解的前提，考查学生发现问题解决问题的能力，是中档题．