题目内容
 已知椭圆
已知椭圆| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
| ||
| 2 |
(1)求椭圆的方程;
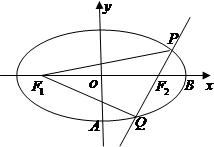
(2)设F1、F2为椭圆的左、右焦点,过F2作直线交椭圆于P、Q两点,求△PQF1的内切圆半径r的最大值.
分析:(1)设出直线的方程,利用直线的截距式写出直线的方程,利用点到直线的距离公式列出关于a,b,c的等式,再利用椭圆的离心率公式得到关于a,b,c的方程组,求出a,b,c的值即得到椭圆的方程.
(2)设出直线方程,将直线方程与椭圆方程联立,利用韦达定理得到关于交点坐标的关系,写出△PQF1的面积并求出最大值,再将面积用外接圆的半径表示,求出半径的最大值.
(2)设出直线方程,将直线方程与椭圆方程联立,利用韦达定理得到关于交点坐标的关系,写出△PQF1的面积并求出最大值,再将面积用外接圆的半径表示,求出半径的最大值.
解答:解:(1)直线AB 的方程为
-
=1即bx-ay-ab=0
由题意得
=1①
∵
=
②
a2=b2+c2③
解得a=
,b=1
∴椭圆的方程为
+y2=1
(2)设PQ:x=ty+
代入
+y2=1
并整理得(t2+3)y2+2
ty-1=0
△=(2
t)2+4(t2+3)>0
设P(x1,y1),Q(x2,y2)则
y1+y2=-
,y1y2=-
∴|y1-y2|=
=
=2
当
=
即t2=1时,|y1-y2|max=
∴S△PQF1=
|F1F2||y1- y2|≤
•2
•
=
又∴S△PQF1=
(|PF1 | +|QF1|+|PQ|)r=
•4
r=2
r
∴rmax=
=
| x |
| a |
| y |
| b |
由题意得
| ab | ||
|
∵
| c |
| a |
| ||
| 3 |
a2=b2+c2③
解得a=
| 3 |
∴椭圆的方程为
| x2 |
| 3 |
(2)设PQ:x=ty+
| 2 |
| x2 |
| 3 |
并整理得(t2+3)y2+2
| 2 |
△=(2
| 2 |
设P(x1,y1),Q(x2,y2)则
y1+y2=-
2
| ||
| t2+3 |
| 1 |
| t2+3 |
∴|y1-y2|=
| (y1+y2)2-4y1y2 |
=
(-
|
=2
| 3 |
-(
|
当
| 1 |
| t2+3 |
| 1 |
| 4 |
| ||
| 2 |
∴S△PQF1=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| ||
| 2 |
| 3 |
又∴S△PQF1=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
∴rmax=
| ||
2
|
| 1 |
| 2 |
点评:求圆锥曲线的方程的一般方法是利用待定系数法;解决直线与圆锥曲线的位置关系一般是将直线的方程与圆锥曲线的方程联立,消去一个未知数得到关于一个未知数的二次方程,利用韦达定理找突破口.

练习册系列答案
相关题目