题目内容
19．
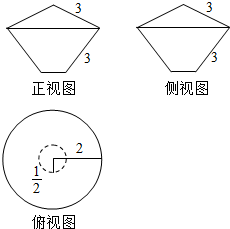根据几何图的表面积（如图所示），求该几何体的表面积．
分析 由已知中的三视图，可得该几何体由一个圆锥和圆台成而成，分别求各个面的面积，相加可得答案．
解答 解：由已知中的三视图，可得该几何体由一个圆锥和圆台成而成，
圆锥的底面半径为2，母线长为3，故圆锥的侧面积为：π×2×3=6π，
圆台的下上底面半径为2，下底面半径为1，母线长为3，故圆台的侧面积为：π×（2+$\frac{1}{2}$）×3=$\frac{15π}{2}$，圆台的底面面积为：$\frac{1}{4}π$，
故组合体的全面积S=6π+$\frac{15π}{2}$+$\frac{1}{4}π$=$\frac{55}{4}π$．
点评 本题考查的知识点是由三视图求体积和表面积，解决本题的关键是得到该几何体的形状．
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
4．f（x）=$\left\{\begin{array}{l}{\frac{{x}^{2}-2x+4}{x}}&{x＞0}\\{-{x}^{2}-2x}&{x≤0}\end{array}\right.$的值域为（ ）
| A． | R | B． | （-∞，1]∪[2，+∞） | C． | [1，2] | D． | （-∞，-1]∪[2，+∞） |