题目内容
4.f(x)=$\left\{\begin{array}{l}{\frac{{x}^{2}-2x+4}{x}}&{x>0}\\{-{x}^{2}-2x}&{x≤0}\end{array}\right.$的值域为( )| A. | R | B. | (-∞,1]∪[2,+∞) | C. | [1,2] | D. | (-∞,-1]∪[2,+∞) |
分析 可分别在每段上求函数f(x)的值域:x>0时,可得到f(x)=$x+\frac{4}{x}-2$,从而根据基本不等式即可得出此时f(x)≥2;而x≤0时,配方便得f(x)=-(x+1)2+1,显然此时f(x)≤1,把这两种情况求得的范围求并集即可得出原函数的值域.
解答 解:①x>0时,f(x)=$\frac{{x}^{2}-2x+4}{x}$=$x+\frac{4}{x}-2≥2$;
当$x=\frac{4}{x}$,即x=2时取“=”;
②x≤0时,f(x)=-(x+1)2+1≤1;
当x=-1时取“=”;
∴综上得原函数的值域为(-∞,1]∪[2,+∞).
故选:B.
点评 考查函数值域的概念,分段函数值域的求法:在每段上求,再求并集,基本不等式的运用,注意判断是否取到“=”,配方求二次函数值域的方法.

练习册系列答案
相关题目
16.已知集合M是由a=x2-y2,x,y∈N得到所有a值组成的,对于元素6和7,( )
| A. | 仅有7∈M | B. | 仅有6∈M | C. | 都属于M | D. | 都不属于M |
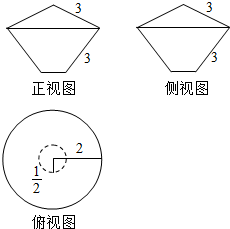 根据几何图的表面积(如图所示),求该几何体的表面积.
根据几何图的表面积(如图所示),求该几何体的表面积.