题目内容
在 中,角
中,角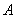 、
、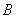 、
、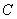 所对的边分别为
所对的边分别为 、
、 、
、 ,若
,若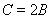 ,则
,则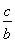 为( )
为( )
A. B.
B.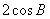 C.
C. D.
D.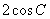
B
【解析】
试题分析:由于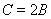 ,故
,故 ,所以
,所以 ,由正弦定理可得
,由正弦定理可得
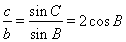 ,故选B.
,故选B.
考点:1.二倍角公式;2.正弦定理

练习册系列答案
相关题目
题目内容
在 中,角
中,角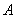 、
、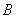 、
、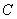 所对的边分别为
所对的边分别为 、
、 、
、 ,若
,若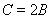 ,则
,则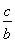 为( )
为( )
A. B.
B.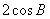 C.
C. D.
D.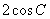
B
【解析】
试题分析:由于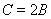 ,故
,故 ,所以
,所以 ,由正弦定理可得
,由正弦定理可得
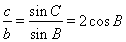 ,故选B.
,故选B.
考点:1.二倍角公式;2.正弦定理
