题目内容
设两个非零向量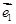 和
和 不共线.
不共线.
(1) 如果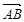 =
=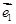 +
+ ,
,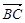 =
=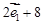
 ,
,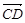 =
=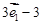
 ,求证:
,求证: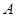 、
、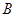 、
、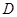 三点共线;
三点共线;
(2) 若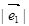 =2,
=2,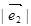 =3,
=3,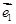 与
与 的夹角为
的夹角为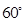 ,是否存在实数
,是否存在实数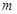 ,使得
,使得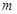
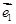
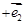 与
与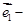
 垂直?并说明理由.
垂直?并说明理由.
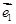 和
和 不共线.
不共线.(1) 如果
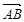 =
=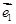 +
+ ,
,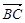 =
=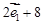
 ,
,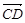 =
=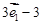
 ,求证:
,求证: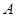 、
、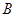 、
、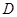 三点共线;
三点共线;(2) 若
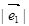 =2,
=2,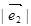 =3,
=3,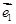 与
与 的夹角为
的夹角为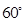 ,是否存在实数
,是否存在实数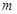 ,使得
,使得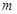
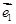
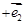 与
与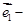
 垂直?并说明理由.
垂直?并说明理由.(1) 证明见解析; (2) 存在实数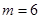 ,使得
,使得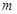
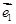
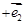 与
与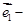
 垂直.
垂直.
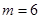 ,使得
,使得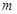
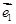
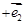 与
与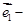
 垂直.
垂直.试题分析:(1)证明三点共线,只需证明三点构成的向量中任意两向量共线即可,由向量的运算
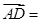
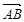 +
+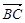 +
+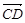
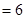
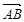 ,所以向量共线,那么三点共线;(2)假设存在实数
,所以向量共线,那么三点共线;(2)假设存在实数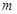 ,使
,使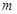
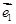
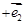 与
与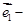
 垂直,那么(
垂直,那么(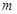
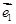
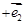 )
) (
(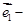
 )=
)=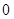 ,又
,又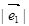 =2,
=2,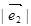 =3,
=3,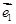 与
与 的夹角为
的夹角为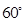 ,将等式展可代入可得关于m的方程
,将等式展可代入可得关于m的方程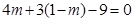 ,得
,得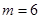 .
.证明:(1)
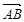 +
+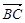 +
+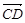 =(
=(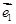 +
+ )+(
)+(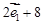
 )+(
)+(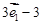
 )
)=6(
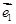 +
+ )=6
)=6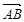 ,
, 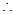
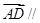
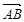 且
且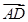 与
与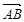 有共同起点.
有共同起点.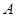 、
、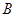 、
、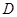 三点共线
三点共线 (2)假设存在实数
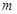 ,使得
,使得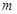
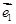
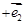 与
与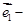
 垂直,则(
垂直,则(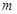
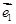
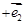 )
) (
(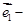
 )=
)=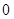
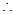
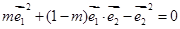
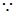
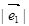 =2,
=2,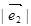 =3,
=3,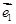 与
与 的夹角为
的夹角为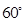
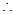
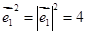 ,
,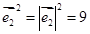 ,
,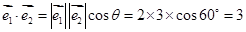
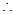
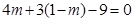
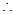
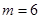 故存在实数
故存在实数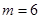 ,使得
,使得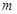
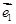
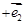 与
与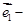
 垂直.
垂直.
练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
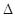 ABC所在平面内一点,且满足:
ABC所在平面内一点,且满足: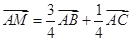 .
.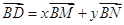 ,求
,求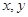 的值.
的值.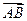 所成的比为-
所成的比为-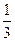 ,则点B分有向线段
,则点B分有向线段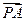 所成的比是
所成的比是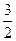
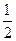

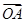 =(1,-2),
=(1,-2),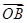 =(a,-1),
=(a,-1),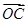 =(-b,0),a>0,b>0,O为坐标原点,若A、B、C三点共线,则
=(-b,0),a>0,b>0,O为坐标原点,若A、B、C三点共线,则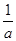 +
+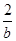 的最小值是________.
的最小值是________.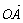 、
、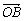 、
、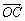 ,其中
,其中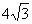 ,若
,若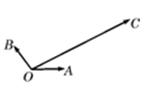
 与
与 均为单位向量,它们的夹角为
均为单位向量,它们的夹角为 ,那么
,那么 等于( )
等于( )


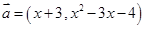 与
与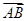 相等,其中
相等,其中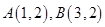 ,则
,则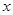 =_________.
=_________. , 若a//b, 则实数m等于
, 若a//b, 则实数m等于
