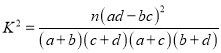题目内容
【题目】已知向量a＝(2x－y＋1，x＋y－2)，b＝(2，－2).
①当x、y为何值时，a与b共线？
②是否存在实数x、y，使得a⊥b，且|a|＝|b|？若存在，求出xy的值；若不存在，说明理由.
【答案】①. 
；②. 
或
.
【解析】试题分析：（1）由a与b共线，可得存在非零实数λ使得a＝λb，从而可得结论；
（2）由a⊥b得，（2x﹣y+1）×2+（x+y﹣2）×（﹣2）=0，由|a|＝|b|得，（2x﹣y+1）2+（x+y﹣2）2=8，从而可得结论.
试题解析：
①∵a与b共线，
∴存在非零实数λ使得a＝λb，
∴
②由a⊥b(2x－y＋1)×2＋(x＋y－2)×(－2)＝0
x－2y＋3＝0.(1)
由|a|＝|b|(2x－y＋1)2＋(x＋y－2)2＝8.(2)
解(1)(2)得
或
∴xy＝－1或xy＝
..
练习册系列答案
相关题目
【题目】为了解人们对于国家新颁布的“生育二胎放开”政策的热度，现在某市进行调查，随机调查了
人，他们年龄大点频数分布及支持“生育二胎”人数如下表：
年龄 |
|
|
|
|
|
| ||
频数 |
|
|
|
|
|
| ||
支持“生育二胎” |
|
|
|
|
|
| ||
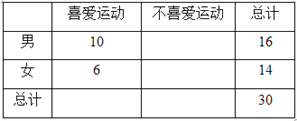
（Ⅰ）由以上统计数据填下面 | 年龄不低于 | 年龄低于 | 合计 | |||||
支持 |
|
| ||||||
不支持 |
|
| ||||||
合计 | ||||||||
（Ⅱ）若对年龄在
的的被调查人中随机选取两人进行调查，恰好这两人都支持“生育二胎放开”的概率是多少？
参考数据： 
， 
.
