题目内容
(本题满分14分)如图,点P在正方形ABCD所在的平面外,PD⊥面ABCD,∠PAD=45°,空间一点E在平面ABCD上的射影是点B,且PB⊥面AEC.
(1)求直线AD与平面AEC所成的角的正切值;
(2)若F是AP的中点,求直线BF与CE所成角.
【答案】
,
【解析】解:
(1)∵在正方形ABCD中AD∥BC,
∴AD与平面AEC所成的角即
为BC与平面AEC所成的角
∵PB⊥面AEC,
∴BC与平面AEC所成的角的余角即为∠PBC,
又BC⊥CD且BC⊥PD,所以BC⊥PC,tan∠PBC==,
设BC与平面AEC所成的角为θ,
则tanθ=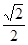 ……………7分
……………7分
(2)∵PB⊥面AEC,∴PB⊥EC,
又空间一点E在平面ABCD上的射影是点B,AB⊥BC,
所以由三垂线定理可以得到AB⊥EC,
故EC⊥面PAB,所以EC⊥BF,
即EC与BF成 ……………14

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目


 、
、 的边长都是1,平面
的边长都是1,平面 平面
平面 在
在 上移动,点
上移动,点 在
在 上移动,若
上移动,若 (
( )
)
 的长;
的长; 为何值时,
为何值时, 与面
与面 所成锐二面角余弦值的大小.
所成锐二面角余弦值的大小. ,又E、F分别是C1A和C1B的中点。
,又E、F分别是C1A和C1B的中点。 (1)求证:EF//平面ABC;
(1)求证:EF//平面ABC; 平面C1CBB1;
平面C1CBB1;