题目内容
已知全集U=R，P={x|a+1≤x≤2a+1}，Q={x|x2-3x≤10}．
（1）若a=3，求（∁UP）∩Q；
（2）若P∩Q=P，求实数a的取值范围．
（1）若a=3，求（∁UP）∩Q；
（2）若P∩Q=P，求实数a的取值范围．
∵Q={x|x2-3x≤10}=[-2，5]．
（1）当a=3时，P={x|a+1≤x≤2a+1}=[4，7]，
∴CUP=（-∞，4）∪（7，+∞）
故（CUP）∩Q=[（-∞，4）∪（7，+∞）]∩[-2，5]=[-2，4）
（2）当a+1＞2a+1，即a＜0时，P=∅⊆Q满足条件P∩Q=P
当a+1≤2a+1，即a≥0时，P≠∅时
若P∩Q=P，则P⊆Q
则
解得0≤a≤2
综上所述实数a的取值范围为（-∞，2]
（1）当a=3时，P={x|a+1≤x≤2a+1}=[4，7]，
∴CUP=（-∞，4）∪（7，+∞）
故（CUP）∩Q=[（-∞，4）∪（7，+∞）]∩[-2，5]=[-2，4）
（2）当a+1＞2a+1，即a＜0时，P=∅⊆Q满足条件P∩Q=P
当a+1≤2a+1，即a≥0时，P≠∅时
若P∩Q=P，则P⊆Q
则
|
解得0≤a≤2
综上所述实数a的取值范围为（-∞，2]
练习册系列答案
一线名师提优试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
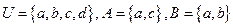，则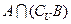
= ▲ 