题目内容
已知圆x2+y2-6mx-2(m-1)y+10m2-2m-24=0(m∈R).
(1)求证:不论m取什么值,圆心在同一直线l上;
(2)与l平行的直线中,哪些与圆相交,相切,相离.
(1)求证:不论m取什么值,圆心在同一直线l上;
(2)与l平行的直线中,哪些与圆相交,相切,相离.
(1)见解析(2)当d<r,即-5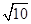 -3<b<5
-3<b<5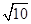 -3时,直线与圆相交;当d=r,即b=±5
-3时,直线与圆相交;当d=r,即b=±5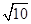 -3时,直线与圆相切;当d>r,即b<-5
-3时,直线与圆相切;当d>r,即b<-5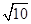 -3或b>5
-3或b>5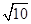 -3时,直线与圆相离.
-3时,直线与圆相离.
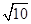 -3<b<5
-3<b<5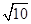 -3时,直线与圆相交;当d=r,即b=±5
-3时,直线与圆相交;当d=r,即b=±5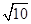 -3时,直线与圆相切;当d>r,即b<-5
-3时,直线与圆相切;当d>r,即b<-5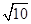 -3或b>5
-3或b>5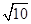 -3时,直线与圆相离.
-3时,直线与圆相离.(1)证明:配方得(x-3m)2+[y-(m-1)]2=25.设圆心为(x,y),则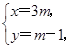 消去m,得x-3y-3=0.故不论m取什么值,圆心在同一直线l:x-3y-3=0上.
消去m,得x-3y-3=0.故不论m取什么值,圆心在同一直线l:x-3y-3=0上.
(2)解:设与l平行的直线为n:x-3y+b=0,则圆心到直线l的距离d=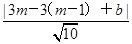 =
=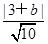 ,由于圆的半径r=5,∴当d<r,即-5
,由于圆的半径r=5,∴当d<r,即-5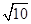 -3<b<5
-3<b<5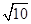 -3时,直线与圆相交;当d=r,即b=±5
-3时,直线与圆相交;当d=r,即b=±5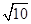 -3时,直线与圆相切;当d>r,即b<-5
-3时,直线与圆相切;当d>r,即b<-5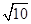 -3或b>5
-3或b>5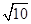 -3时,直线与圆相离
-3时,直线与圆相离
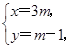 消去m,得x-3y-3=0.故不论m取什么值,圆心在同一直线l:x-3y-3=0上.
消去m,得x-3y-3=0.故不论m取什么值,圆心在同一直线l:x-3y-3=0上.(2)解:设与l平行的直线为n:x-3y+b=0,则圆心到直线l的距离d=
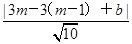 =
=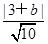 ,由于圆的半径r=5,∴当d<r,即-5
,由于圆的半径r=5,∴当d<r,即-5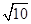 -3<b<5
-3<b<5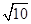 -3时,直线与圆相交;当d=r,即b=±5
-3时,直线与圆相交;当d=r,即b=±5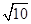 -3时,直线与圆相切;当d>r,即b<-5
-3时,直线与圆相切;当d>r,即b<-5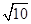 -3或b>5
-3或b>5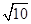 -3时,直线与圆相离
-3时,直线与圆相离
练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
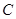 的方程:
的方程: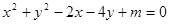
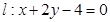 相交于
相交于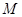 ,
,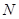 两点,且
两点,且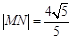 ,求
,求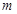 的值
的值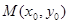 在圆
在圆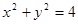 上运动,
上运动,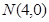 ,点
,点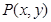 为线段MN的中点.
为线段MN的中点. 的距离的最大值和最小值..
的距离的最大值和最小值..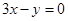 和直线
和直线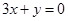 所得弦长分别为
所得弦长分别为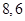 ,求动圆圆心的轨迹方程。
,求动圆圆心的轨迹方程。 是圆
是圆 的直径,
的直径, ,
, 为圆
为圆 .若
.若 ,则
,则


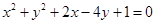 上的任意一点关于直线
上的任意一点关于直线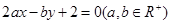 的对称点仍在圆上,则
的对称点仍在圆上,则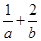 最小值为( )
最小值为( )