题目内容
18.设函数f(x)=$\left\{\begin{array}{l}{{2}^{x}+a,(x>2)}\\{x+{a}^{2},(x≤2)}\end{array}\right.$,若存在x1,x2∈R,且x1≠x2,使得f(x1)=f(x2)成立,则实数a的取值范围是( )| A. | (-∞,-2)∪(1,+∞) | B. | (-∞,-1]∪[2,+∞) | C. | (-∞,-2]∪[1,+∞) | D. | (-∞,-1)∪(2,+∞) |
分析 作出函数f(x)的图象,数形结合,得:2+a2>22+a,由此能求出实数a的取值范围.
解答 解:∵函数f(x)=$\left\{\begin{array}{l}{{2}^{x}+a,(x>2)}\\{x+{a}^{2},(x≤2)}\end{array}\right.$,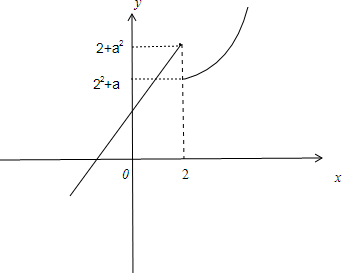
存在x1,x2∈R,且x1≠x2,使得f(x1)=f(x2)成立,
∴可作出如右图所示的函数f(x)的图象,
结合图象得:2+a2>22+a,
∴a2-a-2>0,
解得a<-1或a>2.
∴实数a的取值范围是(-∞,-1)∪(2,+∞).
故选:D.
点评 本题考查实数的取值范围的求法,是中档题,解题时要认真审题,注意数形结合思想的合理运用.

练习册系列答案
相关题目
6.函数y=($\frac{1}{8}$)${\;}^{{x}^{2}-3x-2}$的增区间为( )
| A. | (-∞,$\frac{3}{2}$] | B. | [$\frac{3}{2}$,+∞) | C. | [1,2] | D. | (-∞,1]∪[2,+∞) |
13.集合{x|1<x≤3}用区间形式表示为( )
| A. | [1,3] | B. | (1,3] | C. | [1,3) | D. | (1,3) |