题目内容
14.已知:tan(α+$\frac{1}{4}$β)=x+2,tan(α-$\frac{1}{4}$β)=x+1(x≥-1)(1)当x=1时,求tan2α,tanβ的值;
(2)若对于α≠$\frac{kπ}{2}$+$\frac{π}{4}$(k∈z)的一切α,是否存在实数λ,使λ≤tan2α恒成立,若存在,求λ的取值范围,若不存在,请说明理由.
分析 (1)由条件利用两角和差的正切公式求得tan2α,tanβ的值.
(2)由条件利用两角和差的正切公式求得tan2α的值,再通过换元、利用函数的单调性求得tan2α的最小值,可得λ的取值范围.
解答 解:(1)当x=1时,tan(α+$\frac{1}{4}$β)=x+2=3,tan(α-$\frac{1}{4}$β)=x+1=2,
∴tan2α=tan[(α+$\frac{1}{4}$β)+(α-$\frac{1}{4}$β)]=$\frac{tan(α+\frac{β}{4})+tan(α-\frac{β}{4})}{1-tan(α+\frac{β}{4})•tan(α-\frac{β}{4})}$=$\frac{3+2}{1-3×2}$=-1,
tan$\frac{β}{2}$=tan[(α+$\frac{1}{4}$β)-(α-$\frac{1}{4}$β)]=$\frac{tan(α+\frac{β}{4})-tan(α-\frac{β}{4})}{1+tan(α+\frac{β}{4})•tan(α-\frac{β}{4})}$=$\frac{3-2}{1+3×2}$=$\frac{1}{7}$,
∴tanβ=$\frac{2tan\frac{β}{2}}{1{-tan}^{2}\frac{β}{2}}$=$\frac{\frac{2}{7}}{1-\frac{1}{49}}$=$\frac{7}{24}$.
(2)由于tan2α=tan[(α+$\frac{1}{4}$β)+(α-$\frac{1}{4}$β)]=$\frac{tan(α+\frac{β}{4})+tan(α-\frac{β}{4})}{1-tan(α+\frac{β}{4})•tan(α-\frac{β}{4})}$=$\frac{(x+2)+(x+1)}{1-(x+2)(x+1)}$=$\frac{2x+3}{{-x}^{2}-3x-1}$,
令f(x)=$\frac{2x+3}{{-x}^{2}-3x-1}$=-$\frac{2(x+\frac{3}{2})}{{(x+\frac{3}{2})}^{2}-\frac{5}{4}}$,再令t=x+$\frac{3}{2}$,则f(x)=g(t)=-$\frac{2t}{{t}^{2}-\frac{5}{4}}$=-$\frac{2}{t-\frac{5}{4t}}$.
由于函数y=t-$\frac{5}{4t}$为增函数,故g(t)=-$\frac{2}{t-\frac{5}{4t}}$为增函数.
由x≥-1,可得t≥$\frac{1}{2}$,故当t=$\frac{1}{2}$时,g(t)取得最小值为1,即tan2α的最小值为1.
再根据λ≤tan2α恒成立,可得λ≤1.
点评 本题主要考查两角和差的正切公式,二倍角的正切公式的应用,函数的恒成立问题,属于中档题.

 名校课堂系列答案
名校课堂系列答案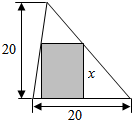 如图,在所示的锐角三角形空地中,新建一个面积不小于75m2的内接矩形池塘(阴影部分),则其一边的长x(单位:m)的取值范围是( )
如图,在所示的锐角三角形空地中,新建一个面积不小于75m2的内接矩形池塘(阴影部分),则其一边的长x(单位:m)的取值范围是( )| A. | [5,15] | B. | [5,10] | C. | [10,15] | D. | [8,18] |
| A. | -$\frac{\sqrt{2}}{2}$ | B. | 0或±$\frac{\sqrt{2}}{2}$ | C. | ±$\frac{\sqrt{2}}{2}$ | D. | 0或$\frac{\sqrt{2}}{2}$ |