题目内容
【题目】如图,在底面为等边三角形的斜三棱柱![]() 中,
中, ![]() ,四边形
,四边形![]() 为矩形,过
为矩形,过![]() 作与直线
作与直线![]() 平行的平面
平行的平面![]() 交
交![]() 于点
于点![]() .
.

(1)证明: ![]() ;
;
(2)若直线![]() 与底面
与底面![]() 所成的角为
所成的角为![]() ,求二面角
,求二面角![]() 的余弦值 .
的余弦值 .
【答案】(1)见解析(2)![]()
【解析】
(1)连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,推导出
,推导出![]() ,由四边形
,由四边形![]() 为平行四边形,得
为平行四边形,得![]() 为
为![]() 的中位线,从而
的中位线,从而![]() 为
为![]() 的中点,由此能证明
的中点,由此能证明![]() ;
;
(2)过![]() 作
作![]() 平面
平面![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,以
,以![]() 为坐标原点,分别以
为坐标原点,分别以![]() 的方向为
的方向为![]() 轴,
轴,![]() 轴,
轴,![]() 轴的正方向建立空间直角坐标系,利用向量法能求出二面角
轴的正方向建立空间直角坐标系,利用向量法能求出二面角![]() 的余弦值.
的余弦值.
解:(1)如图,
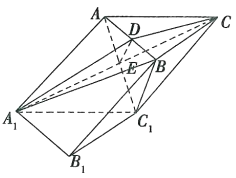
连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
因为![]() 平面
平面![]() 平面
平面![]() ,平面
,平面![]()
平面![]() ,所以
,所以![]() .
.
又四边形![]() 为平行四边形,
为平行四边形,
所以![]() 为
为![]() 的中点,所以
的中点,所以![]() 为
为![]() 的中位线,所以
的中位线,所以![]() 为
为![]() 的中点.
的中点.
又![]() 为等边三角形,所以
为等边三角形,所以![]() .
.
(2)过![]() 作
作![]() 平面
平面![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,设
,设![]() ,
,
则![]() .
.
因为直线![]() 与底面
与底面![]() 所成的角为
所成的角为![]() ,所以
,所以![]() .
.
在![]() 中,因为
中,因为![]() ,
,
所以![]() ,
,![]() .
.
为![]() 平面
平面![]() 平面
平面![]() ,
,
所以![]() ,
,
四边形![]() 为矩形,所以
为矩形,所以![]() ,
,
因为![]() ,所以
,所以![]() .
.
因为![]() 平面
平面![]() 平面
平面![]() ,所以
,所以
![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() .
.
又![]() 为等边三角形,所以
为等边三角形,所以![]() 为
为![]() 的中点.
的中点.
以![]() 为坐标原点,分别以
为坐标原点,分别以![]() 的方向为
的方向为![]() 轴,
轴,![]() 轴,
轴,![]() 轴的正方向建立空间直角坐标系,如图.
轴的正方向建立空间直角坐标系,如图.
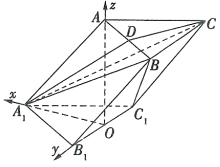
则![]() ,
,![]() ,
,![]() ,
,![]() .
.
因为![]() ,
,
所以![]() ,
,
因为![]() ,
,
所以![]() ,
,
![]() ,
,![]() ,
,
![]() .
.
设平面![]() 的法向量为
的法向量为![]() .
.
由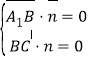 ,得
,得![]() ,
,
令![]() ,得
,得![]() ,
,
所以平面![]() 的一个法向量为
的一个法向量为![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
由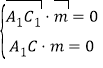 ,得
,得![]() ,
,
令![]() ,得
,得![]() ,
,
所以平面![]() 的一个法向量为
的一个法向量为![]() .
.
所以![]() ,
,
因为所求二面角为钝角,所以二面角![]() 的余弦值为
的余弦值为![]() .
.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案【题目】为比较注射![]() 两种药物产生的皮肤疱疹的面积,选200只家兔作试验,将这200只家兔随机地分成两组,每组100只,其中一组注射药物
两种药物产生的皮肤疱疹的面积,选200只家兔作试验,将这200只家兔随机地分成两组,每组100只,其中一组注射药物![]() ,另一组注射药物
,另一组注射药物![]() .表1和表2所示的分别是注射药物
.表1和表2所示的分别是注射药物![]() 和药物
和药物![]() 后皮肤疱疹面积的频数分布(疱疹面积单位:
后皮肤疱疹面积的频数分布(疱疹面积单位:![]() )
)
表1
疱疹面积 |
|
|
|
|
频数 | 30 | 40 | 20 | 10 |
表2
疱疹面积 |
|
|
|
|
|
频数 | 10 | 25 | 20 | 30 | 15 |
(1)完成图20-3和图20-4所示的分别注射药物![]() 后皮肤疱疹面积的频率分布直方图,并求注射药物
后皮肤疱疹面积的频率分布直方图,并求注射药物![]() 后疱疹面积的中位数
后疱疹面积的中位数

(2)完成下表所示的![]() 列联表,并回答能否有99.9%的把握认为注射药物
列联表,并回答能否有99.9%的把握认为注射药物![]() 后的疱疹面积与注射药物
后的疱疹面积与注射药物![]() 的疱疹面积有差异.(
的疱疹面积有差异.(![]() 的值精确到0.01)
的值精确到0.01)
疱疹面积小于 | 疱疹面积不小于 | 合计 | |
注射药物A |
|
| |
注射药物B |
|
| |
合计 |
附: .
.
P( | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k | 2.706 | 3.811 | 5.021 | 6.635 | 10.828 |