Question

【题目】已知A是圆O：x2+y2＝4上一动点，过点A作AB⊥x轴，垂足为B，动点D满足.

（1）求动点D的轨迹C的方程；

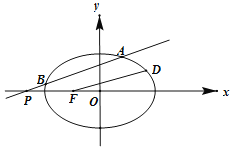
（2）垂直于x轴的直线M交轨迹C于M、N两点，点P（3，0），直线PM与轨迹C的另一个交点为Q.问：直线NQ是否过一定点？若过定点，求出该定点的坐标；若不过定点，请说明理由.

Answer 1

【答案】（1）；（2）直线NQ恒过定点

【解析】

（1）设，用表示出点坐标，代入圆方程化简即可得的轨迹方程；

（2）设直线斜率为，根据根与系数的关系得出的坐标关系，利用两点式表示出直线的方程，化简即可得出结论．

(1)设D(x，y)，∵，∴A(x，)，

代入圆O的方程可得：x24，即1.

∴动点D的轨迹C的方程是：1.

(2)设直线PM的方程为y＝k(x﹣3)，

联立方程组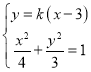，消元得：(3+4k2)x2﹣24k2x+36k2﹣12＝0，

∴△＝576k4﹣4(3+4k2)(36k2﹣12)0，解得：k2.

设M(x1，y1)，Q(x2，y2)，则N(x1，﹣y1)，

由根与系数的关系可得：x1+x2，x1x2，

直线NQ的方程为：，

即(x2﹣x1)y﹣(y1+y2)x+x2y1+x1y2＝0，

∵y1+y2＝k(x1﹣3)+k(x2﹣3)＝k(x1+x2)﹣66，

x2y1+x1y2＝x2k(x1﹣3)+x1k(x2﹣3)＝2kx1x2﹣3k(x1+x2)＝2k3k，

∴直线NQ方程为：(x2﹣x1)0，即(x2﹣x1)＝0，

∴直线NQ恒过定点(，0).